public:omi-5a-o-rech:1._recherche_et

Indexation des documents texte

1. Données texte

Fouille de textes : "Text mining".
Bases de documents : données de type texte ("String").
Algorithmes de recherche sur des documents textes.

1.1 Bases documentaires

$B$ : base documentaire:
- Librairie, bibliothèque, centre de documentation, …
- Dossier contenant des documents (fichiers textes, documents formatés, pages web, forums…)
- Serveur de fichiers (serveur web, fournisseur de contenus, …)
- Moteur de recherche
$n$ : nombre de documents : $n = |B|$.
$d \in B$ : un document appartenant à la base $B$.
$t \in d$ : un terme présent dans le document $d$.

Recherche documentaire :

1.2 Ordres de grandeur

Centre de documentation : $n \in [10^2 - 10^4]$
Fournisseur de contenus (Amazon) : $ n \in [10^4 - 10^8] $
Moteur de recherche (Google) : $ n \in [10^8 - 10^{16}] $

–> "Big data"

1.3 Enjeux

Temps de réponse (< 1s ?)
Stockage des données
Protection des données
Vie privée

1.4 Méthodes

Théorie de l'information
Apprentissage automatique ("Machine Learning")
Reconnaissance de formes
Statistiques

1.5 Exemples de moteurs de recherche

2. Algorithmes sur les textes

Données texte

Recherche/remplacement

Expressions régulières

Appariement, similarité, distance

Arbres d'expressions

3. Principes généraux : double indexation

Fichier inverse - BitMap

On appelle fichier inverse la structure de données qui, à tout terme t, associe l’ensemble D(t) des documents contenant le terme t.

La structure de données implémentant les fichiers inverse est un tableau bidimensionnel binaire $T$ (appelé "bitmap")

A chaque document $d$ est attribué un entier $i \in 1..n$
A chaque terme $t$ est attribué un entier $j \in 1..m$
$T[i,j] = 1 \Leftrightarrow j \in i$
$T[i,j] = 0 \Leftrightarrow j \notin i$
Chaque colonne T[:,j] désigne l'ensemble des documents contenant le terme $j$
Chaque ligne T[i,:] désigne l'ensemble des termes contenus dans le document $i$

Soit $q$ une requête constituée de plusieurs termes $j_1, j_2, ... j_k$.

Cette requête s'interprète comme la recherche des documents contenant à la fois les termes $j_1$ et $j_2, ...$ et $j_k$.

L'ensemble des documents sélectionnés par la requête est donnée par l'opérateur booléen "and": $$ T[:,j_1] \text{ and } T[:,j_2] \text{ and }...\text{ and } T[:,j_k] $$

On note $\{i_1, i_2, ...\}$ la liste des documents sélectionnés par la requête $q$.

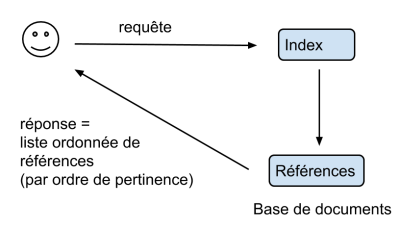
Similarité

Pour chaque document $i$ sélectionné par fichier inverse, on calcule un score de similarité :$$\textbf{sim}(i,q)$$

Les documents sont ensuite classés par ordre décroissant de score. La réponse est une liste ordonnée de documents : $$ (i_1', i_2', ...)$$ avec $\text{sim}(i_1',q) \geq \text {sim}(i_2',q) \geq ...$

4. similarité : approche binaire

Un document $d$ est une liste ordonnée de termes : $d = (d[1], d[2], ..., )$
On cherche une représentation "quantitative" permettant de réaliser des comparaisons entre documents.
L'approche la plus courante : "Bag of words" : on regarde les distribution des fréquence d'occurrence des mots dans un texte sans se préoccuper de leur position dans le texte.

Représentation ensembliste des documents

un document $d$ est représenté par l'ensemble des termes qu'ils contient (sans se préoccuper de leur ordre)

Similarité de Jaccard

Soient deux ensembles A et B.

L'indice de Jaccard est le rapport entre la cardinalité (la taille) de l'intersection des ensembles considérés et la cardinalité de l'union des ensembles. Il permet d'évaluer la similarité entre deux ensembles: $$ J(A,B) = \frac{|A \cap B|}{|A \cup B|} $$

Représentation vectorielle des documents

Un document $d$ est représenté par sous la forme d'un vecteur binaire $\boldsymbol{x}$ de dimension $m$
$m$ est la taille du vocabulaire
Chaque terme $t \in V$ est indexé par un entier $i \in 1..m$
$x_i = 1 \Leftrightarrow i \in d$
$x_i = 0 \Leftrightarrow i \notin d$

Similarité vectorielle

Similarité basée sur la distance :
- Distance vectorielle :
  - distance de Hamming :

$$ \text{dist}(\boldsymbol{x},\boldsymbol{y}) = \sum_{i \in 1..m} |x_i - y_i|$$

Similarité :

$$ \text{sim}(\boldsymbol{x},\boldsymbol{y}) = \frac{1}{1 + \text{dist}(\boldsymbol{x},\boldsymbol{y})}$$

Similarité du cosinus :

$$ \text{sim}(\boldsymbol{x},\boldsymbol{y}) = \frac{ \boldsymbol{x}.\boldsymbol{y} } {||\boldsymbol{x}|| \times ||\boldsymbol{y}||}$$

5. Statistiques sur les textes

On dispose d’une base $B$ de $n$ documents textes.

On note $B = \{d_1,d_2,...\}$, où chaque $d_i$ représente un document différent de la base.

Les documents sont écrits dans un langage $L$ obéissant à un vocabulaire $V$.

On note $V = \{t_1, t_2, ... \}$ où chaque $t_i$ est un terme du vocabulaire $V$.

On note $A$ l'alphabet : ensemble des symboles (caractères) utilisés par le langage $L$.

On note $\alpha \in A$ un caractère de l'alphabet $A$.

Soit $d$ un document de $B$. Il peut être décrit comme :

une suite de symboles : $d = (\alpha_1, \alpha_2, ...)$ avec $\alpha_i \in A$.
ou une suite de mots : $d = (t_1, t_2, ...)$ avec $t_i \in V$.

Statistiques sur les lettres

Statistiques sur les termes

6. Représentation vectorielle

Un document $d$ est représenté par sous la forme d'un vecteur réel $\boldsymbol{x}$ de dimension $m$
$m$ est la taille du vocabulaire
Chaque terme $t \in V$ est indexé par un entier $j \in 1..m$
$x_j = h(j,d) \Leftrightarrow j \in d$
- h(j,d) correspond :
  - à la fréquence de $j$ dans $d$ :

$$f_d(j)$$

au score TF-IFD de $j$ dans $d$ :

$$ - f_d(j) \log g_B(j)$$

$x_j = 0 \Leftrightarrow j \notin d$$

Comparaison vectorielle

Similarité euclidienne
- distance euclidienne :

$$ \text{dist}(\boldsymbol{x},\boldsymbol{y}) = \sqrt{\sum_{i \in 1..m} (x_i - y_i)^2}$$

similarité euclidienne :

$$ \text{sim}(\boldsymbol{x},\boldsymbol{y}) = \frac{1}{1 + \text{dist}(\boldsymbol{x},\boldsymbol{y})}$$

Similarité du cosinus :

$$ \text{sim}(\boldsymbol{x},\boldsymbol{y}) = \frac{ \boldsymbol{x}.\boldsymbol{y} } {||\boldsymbol{x}|| \times ||\boldsymbol{y}||}$$

7. Recherche Web

PageRank

Le World Wide Web (www) est un réseau

formé de documents (les pages html) hébergées sur des serveurs,
les serveurs sont localisés à l'aide de leur adresse (url : universal ressource locator)
les documents sont liés entre eux par des liens hypertextes.

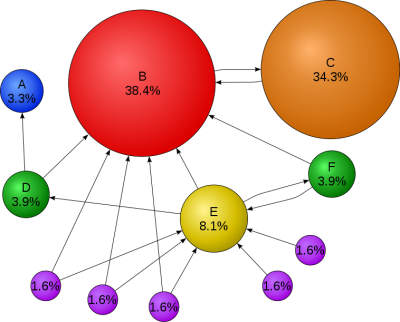
Les algorithmes d'indexation utilisés par les principaux moteurs de recherche prennent en compte la popularité des différentes pages~; les pages les plus "populaires" reçoivent un score plus élevé qui a tendance à les faire apparaître en premier dans la liste des réponses, selon:

$$\text{score}(i,q) = \text{PR}(i) \times \text{sim}(i,q)$$ où $\text{PR}(i)$ est la popularité de la page $i$.

Le score de popularité le plus célèbre est le "Page Rank", proposé par Larry Page, co-fondateurs de Google.

Le calcul du Page Rank repose sur un modèle de parcours aléatoire de graphes. On considère un internaute se déplaçant sur le Web de manière aléatoire. A chaque page visitée, il suit un lien au hasard et répète cette opération un nombre indéfini de fois. Le résultat est un chemin aléatoire sur le graphe. Au cours de ce parcours, certains sites seront visités plus souvent que d'autres car il y a en moyenne plus de chemins qui y conduisent.

Concrètement, le comportement de l'internaute est le suivant~:

A chaque page visitée
- dans q% des cas, suivre un lien au hasard
- dans (1-q)% des cas, choisir une page quelconque du réseau sans suivre de lien particulier.

q est appelé le terme d'amortissement, fixé en pratique à 0.85.

Le graphe est constitué de $n$ nœuds où chaque nœud est une page web. On considère que chaque page est indexée par un indice $i \in 1..n$.

Dans ce cas, le graphe peut être représenté par une matrice $G$ de taille $n \times n$ contenant des 1 et de 0, telle que la valeur 1 signale la présence d'un lien et la valeur 0 l'absence de lien. $G$ a une structure de matrice creuse (beaucoup de 0, peu de 1)

$$G = \left( \begin{array}{ccccccccccc} 1& & & & & & & & & & \\ &1&1& & & & & & & & \\ &1&1& & & & & & & & \\ 1&1& &1& & & & & & & \\ &1& &1&1&1& & & & & \\ &1& & &1&1& & & & & \\ &1& & &1& &1& & & & \\ &1& & &1& & &1& & & \\ &1& & &1& & & &1& & \\ & & & &1& & & & &1& \\ & & & &1& & & & & &1\\ \end{array} \right) $$ (La valeur 0 n'est pas représentée)

On peut de même définir une matrice de transition $P$ contenant les probabilités de transition d'une page à l'autre. $$P = \left( \begin{array}{ccccccccccc} 1& & & & & & & & & & \\ &\frac{1}{2}&\frac{1}{2}& & & & & & & & \\ &\frac{1}{2}&\frac{1}{2}& & & & & & & & \\ \frac{1}{3}&\frac{1}{3}& &\frac{1}{3}& & & & & & & \\ &\frac{1}{4}& &\frac{1}{4}&\frac{1}{4}&\frac{1}{4}& & & & & \\ &\frac{1}{3}& & &\frac{1}{3}&\frac{1}{3}& & & & & \\ &\frac{1}{3}& & &\frac{1}{3}& &\frac{1}{3}& & & & \\ &\frac{1}{3}& & &\frac{1}{3}& & &\frac{1}{3}& & & \\ &\frac{1}{3}& & &\frac{1}{3}& & & &\frac{1}{3}& & \\ & & & &\frac{1}{2}& & & & &\frac{1}{2}& \\ & & & &\frac{1}{2}& & & & & &\frac{1}{2}\\ \end{array} \right) $$

Le calcul du page Rank est fondé sur une estimation de la proportion de temps passée sur chaque site en suivant ce principe.

Il correspond à la mesure stationnaire de la chaîne de Markov associée, définie comme le vecteur $\boldsymbol{x}$ positif et de somme 1 vérifiant~: $$\boldsymbol{x} = \boldsymbol{x}Q^T$$ avec~ $$Q = qP + \frac{(1-q)}{n} \boldsymbol{1}$$ avec $\mathbf{1}$ matrice de taille $n \times n$ ne contenant que des 1.

En pratique :

Le graphe étant de grande taille, il n'est pas possible de résoudre directement l'équation de récurrence
Le graphe est régulièrement mis à jour pour prendre en compte les évolution du Web et de la popularité des différentes pages.

La mise à jour du graphe et du PageRank se fait de manière itérative à l'aide d'un "robot" qui parcourt le web de manière aléatoire et actualise le score de chaque page qu'il visite.

Algo :

Initialiser le vecteur $\boldsymbol{x}$ à la valeur $(1/n,1/n, ..., 1/n)$
Pour chaque page visitée $i$ :
1. Mettre à jour les valeurs des liens sortants : $$ \forall j : i \rightarrow j, P_{ij} \leftarrow \frac{1}{\sum_{j : i \rightarrow j}1} $$
2. choisir une page $j$ au hasard parmi les liens sortants
3. Mettre à jour le score $x_j$ de la page $j$ en fonction des liens entrants, i.e. $$ x_j \leftarrow q \sum_{i:i\rightarrow j} P_{ij} x_i + \frac{1-q}{n}$$

8. Classification

TODO

Table des matières