Dans ce TP nous allons décrire le comportement d'un agent se déplaçant aléatoirement dans un environnement très simple.

Pour établir développer des algorithmes d’apprentissage par renforcement, il est nécessaire de caractériser deux entités:

• Un agent : l'agent est la partie du code qui implémente le plan d'actions (ou "politique"). Il a la capacité :
  • de percevoir son environnement (à l'aide d'observations)
  • d'agir sur son environnement à l'aide d'actions
  • $-->$ la politique décide des choix d'actions en fonction des observations
• Un environnement :
  • Il s'agit d'un simulateur du monde extérieur à l'agent. Il réagit aux actions de l'agent en modifiant son état.
  • L'environnement transmet à l'agent deux types de signaux :
    • les observations
    • les récompenses (gratification des actions)

Nous allons regarder comment programmer ces deux entités pour pouvoir réaliser des simulations simples.

Dans un projet pycharm, vous commencerez par développer deux classes : la classe Agent et la classe Environnement.

On considère ici que les simulations se déroulent sur un nombre limité de pas de temps (ici 10).

Voici le constructeur :

class Environment:
    def __init__(self):
        self.state = 0
        self.steps_left = 10

Dans le cas général, l'environnement initialise également son état. Dans ce cas simple, l'état est un simple compteur qui limite le nombre de pas de temps.

L'état de l'environnement est lu à l'aide de la méthode get_observation(). Il s'agit habituellement d'une fonction de l'état courant (la mesure). On suppose ici que la méthode retourne directement l'état courant (environnement totalement observable):

def get_observation(self):
    return self.state

La méthode get_actions() permet à l'agent de connaître la liste des actions qu'il peut exécuter. Normalement, le jeu d'actions peut changer au cours du temps, certaines actions devenant impossibles dans certains état. Ici seules deux actions sont possibles, encodées par les entiers 0' et 1.

def get_actions(self):
    return [0, 1]

La méthode is_done() signale la fin de l'épisode (atteinte lorsque le compteur vaut 0).

def is_done(self):
    return self.steps_left == 0

Enfin, la méthode action() fait évoluer l'état de l'environnement en fonction des actions de l'agent. Dans le cas général, la méthode modifie l'état en fonction de l'action passée en paramètre, et retourne le signal de récompense. De plus, le nombre de pas est mis à jour afin que la simulation s'arrête lorsque la limite est atteinte.

def action(self, action):
    if self.is_done():
        raise Exception("Game is over")
    self.steps_left -= 1
    return random.random()  

La classe Agent est plus simple et ne contient que deux méthodes :

• le constructeur
• la méthode de mise à jour qui effectue une itération de l'environnement

Voici le constructeur. Il contient un compteur qui conserve le nombre total e récompenses accumulées.

class Agent:
    def __init__(self):
        self.total_reward = 0.0

La méthode de mise à jour prend comme argument une instance d l'environnement et effectue les opérations suivantes :

• observer l'environnement
• lire le répertoire d'actions possibles
• choisir une action et la transmettre à l'environnement
• lire la récompense et mettre à jour le compteur

def step(self, env):
    current_obs = env.get_observation()
    actions = env.get_actions()
    reward = env.action(random.choice(actions))
    self.total_reward += reward

Créez maintenant un programme principal qui crée les deux classes et exécute un épisode :

env = Environment()
agent = Agent()
 
while not env.is_done():
    agent.step(env)
 
print("Total reward got: %.4f" % agent.total_reward)

Faites tourner cet environnement plusieurs fois et vérifiez que la somme des récompenses obtenues varie à chaque fois.

Les mondes-grilles (Grid worlds) permettent de simuler de petits labyrinthes dans lesquels les actions de l'agent se limitent souvent à des déplacements dans les quatre directions cardinales (Nord, Sud, Est et Ouest), un peu comme dans le jeu Pacman. Ils ont l'avantage de présenter un nombre limité d'états et de traiter les problèmes d'apprentissage à l'aide de tables de correspondance (Look-up Tables). Les cases contiennent des récompenses ou des pièges qui doivent être attrapés ou évités par l'agent.

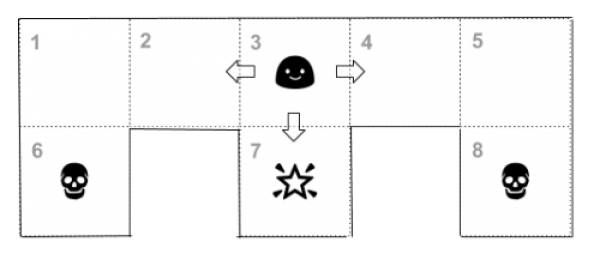
Nous considérons ici un labyrinthe extrêmement simple à 8 cases :

• L'état est défini comme la position de l'agent sur la grille. Il peut donc prendre 8 valeurs possibles et l'espace d'état est l'ensemble discret constitué par les 8 numéros de cases:

$$\mathcal{S} = \{1, 2, 3, 4, 5, 6, 7, 8\}$$

• Les actions correspondent aux mouvements de l'agent sur la grille. L'espace des actions est constitué par les quatre directions cardinales :

$$\mathcal{A} = \{N, S, E, W\}$$

• Les cases 1, 2, 3, 4, et 5 n'apportent aucune récompense. Par contre les cases 6 et 8 apportent une pénalité de -10 et la case 7 apporte un bonus de +10.

Nous allons modifier pas à pas le squelette d'agent et d'environnement précédent pour pouvoir simuler les déplacements d'un agent sur un tel monde.

L'évolution de l'environnement dépend à la fois de l'état courant et de l'action choisie. Ainsi si l'état courant est 3 et l'action est "E" alors l'état prend la valeur 4 et la récompense est 0.

• 1. Le changement d'état et le calcul de la récompense seront implémentés au sein de la méthode action().

next = {
    1 : {"S" : 6, "E" : 2},
    2 : {"W" : 1, "E" : 3},
    3 : {"W" : 2, "S" : 7, "E" : 4},
    4 : {"W" : 3, "E" : 5},
    5 : {"W" : 4, "S" : 8},
    6 : {"N" : 1},
    7 : {"N" : 3},
    8 : {"N" : 5}
    }

reward = {1: 0, 2: 0, 3: 0, 4: 0, 5: 0, 6: -10, 7: 10, 8: -10} 

• 2. Pour l'initialisation, on suppose que la position initiale de l'agent est choisie aléatoirement parmi les 5 premières positions

def __init__(self):
    self.state = random.randint(1,5)
    self.steps_left = 10 

• 3. La méthode get_actions() prend en compte la valeur de l'état (self.state) pour déterminer le jeu d'actions possibles à partir de la table de correspondance next.

Pour l'agent, pas de changement! Il continue de choisir ses actions au hasard.

Dans le programme principal, effectuer un total de 100 simulations et calculer la moyenne et l'écart-type de la récompense totale.

Afin de rendre notre agent un peu plus "intelligent", nous allons calculer une "fonction de valeur" qui estime le caractère "propice" ou "funeste" d'un état à partir de la récompense cumulée moyenne obtenue à partir de cet état.

Si $s_t$ est l'état à l'instant $t$ : $$V(s_t) = E(\sum_{t'=t}^T r_{t'})$$ avec $T$ l'instant final (fin de l'épisode)

Il est nécessaire pour cela d'ajouter à l'agent une liste les états parcourus au cours de l'épisode. Cette liste est appelée la trace.

Ainsi, le constructeur de l'agent devient :

class Agent:
    def __init__(self):
        self.total_reward = 0.0
        self.trace = []

Cette trace doit être mise à jour à chaque itération pour obtenir en fin d'épisode la liste de tous les états parcourus.

Pour calculer (de façon simplifiée) la fonction de valeur, nous utiliserons l'algorithme suivant :

V = {1 :0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0} 
nb_visites = {1 :0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0} 
total_reward_sum = {1 :0, 2: 0, 3: 0, 4: 0, 5: 0, 6: 0, 7: 0, 8: 0} 
pour i de 1 à N:
    exécuter un épisode
    pour tout s dans agent.trace :
        nb_visites[s] += 1
        total_reward_sum[s] += agent.total_reward
pour tout s dans V:
    V[s] = total_reward_sum[s] / nb_visites[s]   

Pour calculer la fonction de valeur, on utilisera N = 100

Pour améliorer sa récompense moyenne, l'agent va maintenant prendre en compte la valeur de l'état futur pour choisir l'action, autrement dit, si $s_t$ est l'état courant : $$a_t = \underset{a \in \mathcal{A}}{\text{argmax }} V(\text{next}(s_t, a))$$

• Écrire une méthode step_valeur() dans laquelle l'action est choisie selon la fonction de valeur (et non plus aléatoirement)

def step_valeur(self, env, V):
    ...

• Lancer des simulations avec cette nouvelle méthode de mise à jour et calculer la récompense moyenne obtenue sur 100 épisodes et comparer au résultat précédent. Conclusion?

Le calcul exact de la fonction de valeur nécessite de mémoriser l'historique complet des récompenses. Au lieu de conserver la somme des récompenses, on conserve la liste des récompenses obtenues.

class Agent:
    def __init__(self):
        self.rewards = []
        self.trace = []

et la mise à jour se fait en ajoutant les récompenses en fin de liste :

def step(self, env):
    ...
    self.rewards += [reward]

En fin de simulation, la valeur cumulée est calculée séparément pour chaque état rencontré:

• pour chaque état $s_t$ de la trace :
  • calculer la somme des récompenses présente et futures
  • ajouter la valeur dans total_rewards_sum
  • incrémenter le nombre de visites

Calculer à nouveau la fonction de valeur et comparer la politique obtenue à la politique précédente.