Table des matières
RECHERCHE D'INFORMATION
1. Généralités
1.1 Base de textes
Une bases de textes est un ensemble constitué de plusieurs textes.
Exemples :
- Bases de documents, dossiers contenant des documents, …
- Collections de livres (électroniques)
- Contenus en ligne (descriptifs de films, articles de journaux, descriptifs de produits.)
- Messageries, blogs, forums
- Ensemble du web (les pages web étant vues comme du texte mis en forme au format html).
On note :
- $d \in B$ : un document appartenant à la base $B$.
- $t \in d$ : un terme présent dans le document $d$.
On dispose d’une base $B$ de $n$ documents textes. Une base documentaire $B$ est un ensemble de documents.
On note $B = \{d_1,d_2,...\}$, où chaque $d_i$ représente un document différent de la base.
$n$ est le nombre de documents de la base : $n = |B|$.
- Centre de documentation : $n \in [10^2 - 10^4]$
- Fournisseur de contenus (Amazon) : $ n \in [10^4 - 10^8] $
- Moteur de recherche (Google) : $ n \in [10^8 - 10^{16}] $
Les documents sont écrits dans un langage $L$ obéissant à un vocabulaire $V$.
On note $V = \{t_1, t_2, ... \}$ où chaque $t_k$ est un terme du vocabulaire $V$.
$K$ est la taille du vocabulaire : $K = |V|$.
On note $A$ l'alphabet : ensemble des symboles (caractères) utilisés par le langage $L$.
On note $\alpha \in A$ un caractère de l'alphabet $A$.
Un document texte pourra être décrit soit comme :
- une séquence de caractères (lettres)
- une séquence de termes (mots)
Soit $d$ un document de $B$. Il peut être décrit comme :
- une suite de symboles : $d = (\alpha_1, \alpha_2, ...)$ avec $\alpha_i \in A$.
- ou une suite de mots : $d = (t_1, t_2, ...)$ avec $t_i \in V$.
1.2 Recherche d'information
Les algorithmes que l’on va étudier portent sur la recherche d'informations dans des bases de textes. Cette recherche repose essentiellement sur l'utilisation de mots-clés
La recherche dans les bases de textes nécessite la mise en oeuvre d'algorithmes spécifiques. On parle de recherche par le contenu (par opposition à une recherche basée sur les étiquettes de données indexées/structurées)
Exemples :
- Recherche de textes contenant le terme : “artichaud”
- Recherche d’un motif (expression régulière) : une adresse email, une URL, un expéditeur, un numéro tel
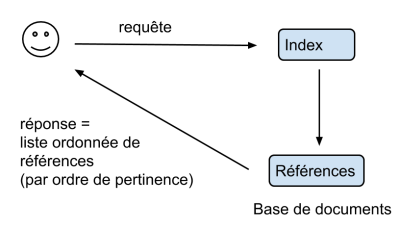
$\rightarrow$ La réponse de l’algorithme est une liste ordonnée de références, classée d’après la pertinence des résultats (≃ similarité)
1.3 Problématiques de la recherche de texte
- performance du programme, il faut considérer deux notes et non pas une seule. La performance d’un programme se mesure sur un axe (précision, rappel).
- temps de réponse des algorithmes : l’utilisateur classique veut attendre moins de 2 à 3 secondes. Sur des bases extrêmement grandes (type recherche web), il faut donc être très performant pour atteindre ces temps de réponses.
- Stockage des données : intégralité des textes ou simple descriptif/résumé?
- Les moteurs de recherche par exemple ne stockent aucune page web, ils ne stockent que des index et des références.
- On parle de “Big Data"
- Protection des données et vie privée : la recherche par le contenu a accès au contenu des documents (textes, messages, notes), qui peuvent contenir des informations à caractère privé. L’indexation de ces textes et messages doit être fait avec le consentement de l'utilisateur, qui n'est pas toujours conscient des enjeux liés à la collecte des données privées.
1.4 Méthodes
- Théorie de l'information
- Apprentissage automatique ("Machine Learning")
- Reconnaissance de formes
- Statistiques
1.5 Exemples de moteurs de recherche
2. Similarité entre documents
Pour mettre en oeuvre la recherche dans les bases de textes, on a besoin d'une métrique permettant de mesurer la similarités entre plusieurs documents.
Plus le score de similarité entre deux documents est élevé, plus les documents sont proches (du point de vue de leur "contenu").
Les scores de similarité sont en général normalisés (entre 0 et 1 ou entre -1 et 1)
Les distances classiques entre chaines de caractères étant inopérantes pour des textes de grande taille, on utilise en général une approche ensembliste/statistique.
- Un document $d$ est une liste ordonnée de termes : $d = (d[1], d[2], ..., )$
- On cherche une représentation "quantitative" permettant de réaliser des comparaisons entre documents.
- L'approche la plus courante : "Bag of words" : on regarde les distribution des fréquence d'occurrence des mots dans un texte sans se préoccuper de leur position dans le texte.
2.1 Approche ensembliste
un document $d$ est représenté par l'ensemble des termes qu'ils contient (sans se préoccuper de leur ordre ni de leur répétition éventuelle)
Soient deux ensembles A et B.
L'indice de Jaccard est le rapport entre la cardinalité (la taille) de l'intersection des ensembles considérés et la cardinalité de l'union des ensembles. Il permet d'évaluer la similarité entre deux ensembles: $$ J(A,B) = \frac{|A \cap B|}{|A \cup B|} $$
Dans le cas où A et B sont des ensembles de termes, deux documents qui utiliseraient exactement les mêmes termes (mais pas dans le même ordre) auraient une similarité de 1 tandis que deux documents utilisant un vocabulaire strictement différent auraient une similarité de 0.
On notera que par construction, l'indice de Jaccard permet de comparer des documents de taille très différentes. L'utilisation d'un même vocabulaire (le même champ lexical) indique que les documents sont proches thématiquement.
texte 1 = "Deux heures plus tard, je le rencontre devant la gare Saint- Lazare. Il est avec un camarade qui lui dit : "tu devrais faire mettre un bouton supplémentaire à ton pardessus."
texte 2 = "Deux heures après, je le revois devant la gare Saint-Lazare. Il est avec un ami qui lui conseille de coudre un bouton à son pardessus."
(indication : "Saint"-"Lazare" compte comme deux termes)
2.2 Approche basée sur les fréquences
L'approche ensembliste reste assez rudimentaire, elle ne prend pas en compte la fréquence d'apparition des différents termes de vocabulaire à l'intérieur du document.
L'approche basée sur les fréquences fait au contraire un comptage précis du nombre d'apparitions de chaque terme de vocabulaire.
- Soit
docun document contenantTmots. - Soit
cptle dictionnaire qui compte le nombre d’apparitions de chaque mot. - Soit
freqle dictionnaire qui compte la fréquence d’apparition de chaque mot.
cpt = {} for mot in doc : if mot not in cpt: cpt[mot] = 1 else: cpt[mot] += 1 freq = {} for mot in cpt : freq[mot] = cpt[mot]/T
Remarque : la somme des fréquences vaut 1.
Comparaison d'histogrammes de fréquence
Soit un message $d$ constitué de $T$ mots ($d_1$, …, $d_i$, …, $d_T$). Chaque mot appartient à un vocabulaire $V = \{t_1,...,t_K\}$ de taille $K$.
Pour effectuer une comparaison basée sur les fréquences d'apparition, on indexe chaque terme de vocabulaire $t \in V$ par un indice (unique) $k$.
Pour tout $t \in V$, on note $f(t,d)$ la fréquence du terme $t$ dans le document $d$.
- Un document $d$ est représenté sous la forme d'un vecteur réel $\boldsymbol{x} \in \mathbb{R}^K$
- (avec $K$ la taille du vocabulaire)
- A tout terme $t \in V$ on associe son index $k \in 1..K$ :
- $x_k = f(t,d) \Leftrightarrow t \in d$
- $x_k = 0 \Leftrightarrow t \notin d$
Remarque : $\mathbf{x}$ est un vecteur “creux”. Il contient beaucoup de 0 (le vocabulaire utilisé dans un texte est de taille ≪ K).
- ⇒ passage d’une information qualitative à une information quantitative.
- ⇒ Des textes peuvent être :
- voisins
- colinéaires
- orthogonaux
- etc…
- tout comme des vecteurs de $\mathbb{R}^K$
En particulier, on peut avec cette approche définir une distance euclidienne entre textes:
Plus intéressante, la similarité du cosinus permet de regarder la "colinéarité" entre deux vecteurs de $\mathbb{R}^K$ indépendamment de leur norme :
- Deux textes "colinéaires" ont un sore de similarité cosinus égal à 1
- Par exemple, deux textes utilisant un vocabulaire proche mais de taille (norme) tres différente peuvent avoir un score de similarité (colinéarité/cosinus) proche de 1.
- Deux textes "orthogonaux" ont un sore de similarité cosinus égal à 0
2.3 Fréquence documentaire
- les plus fréquents :
"le","la","un","des" - très fréquent :
"petit","manger","prendre","donner" - assez fréquent :
"poire","soleil","examiner","échanger" - …
- très rare :
"pédoncule","astrolabe"
Loi de Zipf
- soit $V$ l’ensemble du vocabulaire. On note pour tout $t$ appartenant à $V$ : $f(t)$ est la fréquence du terme $t$.
- $r(t)$ : rang du terme $t$ (les termes sont ordonnés selon les fréquences décroissantes).
Loi de Zipf : la fréquence d’un terme est inversement proportionnelle à son rang.
Il s'agit d'une distribution de type “loi de Puissance”.
remarque : pour une base de textes donnée, on peut estimer la constante C en traçant les fréquence mesurées empiriquement selon une échelle logarithmique (log®, log(f))
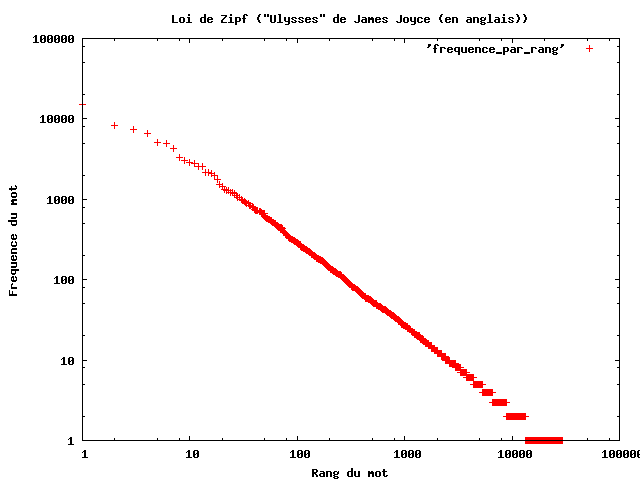 Fréquence des mots en fonction du rang dans la version originale d'Ulysse de James Joyce (source : Wikipedia.org).
Fréquence des mots en fonction du rang dans la version originale d'Ulysse de James Joyce (source : Wikipedia.org).
Interprétation :
- très peu de mot apparaissent très souvent
- beaucoup de mots apparaissent très peu souvent
Du point de vue de la théorie de l’information :
- Les termes courants apportent peu d’informations
- Les termes peu courants apportent beaucoup d’informations.
TF-IDF
Il est possible à partir de l’étude de fréquence de définir un seuil pour sélectionner les termes les plus “informatifs”.
Voir également : statistiques_sur_les_lettres
Dans le cadre des bases de documents, on appelle fréquence documentaire $g(t)$ d’un terme $t$ la fréquence d’apparition du terme dans les différents documents de la base $B$.
Où |{d:t dans d}| est le nombre de documents contenant $t$ et $|B|$ est la taille de la base.
Exemples :
- $g(t) = 1$ : le terme est présent dans tous les documents
- $g(t) = 0,5$ : le terme est présent dans 1 document sur 2
- $g(t) = 1/n$ : le terme est présent dans 1 seul document
On peut sur le même principe mesurer l’information documentaire apportée par le terme $t$ comme :
ici, $I(t)$ représente la capacité du terme $t$ à “séparer” les documents de la base.
Ainsi, les termes apportant $I$ bits d’information permettent de réaliser $I$ partitions de la base (pour extraire des sous-ensembles de taille $|B| / 2I$ )
On remarque que
- si le terme est présent dans tous les documents, son information documentaire est nulle.
- si le terme est présent dans un seul document, son information documentaire est maximale.
En pratique, l'information documentaire $-\log_2(g(t))$ définit le ``poids'' du terme $t$ : plus elle est élevée, plus le terme est `rare' (ou spécifique) et donc intéressant du point de vue de la recherche documentaire.
En recherche d’information, on utilise fréquemment un encodage vectoriel des textes nommé TF-IDF (= term frequency - Inverse Document Frequency).
Soit $d$ un document appartenant à $B$. Pour tout $t$ appartenant à $d$ : $$\text{TF-IDF}(t,d) = -f(t,d)log(g(t)) $$
- où $f(t,d)$ est la fréquence du terme $t$ dans $d$
- et $g(t)$ est la fréquence documentaire de $t$ dans $B$.
La transformation TD-IDF traduit alors un texte $d$ en un vecteur $\boldsymbol{x}$ appartenant à $\in \mathbb{R}^K$ selon le principe vu précédemment:
- A tout terme $t \in V$ on associe son index $k \in 1..K$ :
- $x_k = \text{TF-IDF}(t,d) \Leftrightarrow t \in d$
- $x_k = 0 \Leftrightarrow t \notin d$
Le codage TF-IDF est utilisé principalement :
- Dans les moteurs de recherche
- Dans la classification automatique de documents