restricted:cm3

−Table des matières

4. Moteurs de recherche

4. Moteurs de recherche

Les algorithmes que l’on va étudier portent sur la recherche d'informations dans des bases de textes. Cette recherche repose essentiellement sur l'utilisation de mots-clés.

Notation : $q = \{t_1, t_2, …\}$ ← liste de termes

Exemples :

Recherche de textes contenant le terme : “artichaud”
Recherche de textes contenant les terme : "météo", "marine", "marseille"

Recherche documentaire :

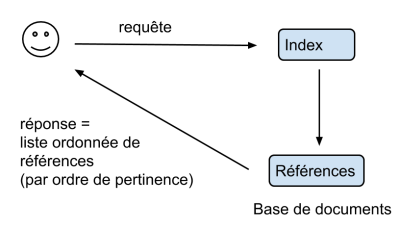
La réponse du serveur est une liste ordonnée de références vers des documents de la base par ordre décroissant de pertinence.

NB: on considère que la pertinence repose ici sur la similarité entre la requête et le document

Un algorithme de recherche d'informations est constitué de trois étapes:

Sélection : les documents conformes à la requête
Similarité : score brut basé sur la similarité requête/document
Pondération : prise en compte de critères supplémentaires : popularité, etc…

4.1. Sélection

Soit $q$ une requête constituée de $k$ termes : $t_1$ , …, $t_k$ .

On note $D_t \subset B$ l'ensemble des documents contenant $t$ .

L'ensemble de documents sélectionnés par la requête est $D_{t_1}\cap...\cap D_{t_k}$

Fichier inverse

On appelle fichier inverse la structure de données qui, à tout terme $t$ , associe l’ensemble $D(t)$ des références vers les documents contenant le terme $t$ .

$t \rightarrow D(t)$

$t$ est la clé
$D(t)$ est une liste de références

On parle de multi-indexation (par opposition à l'indexation simple qui associe une clé à une référence)

Index BitMap

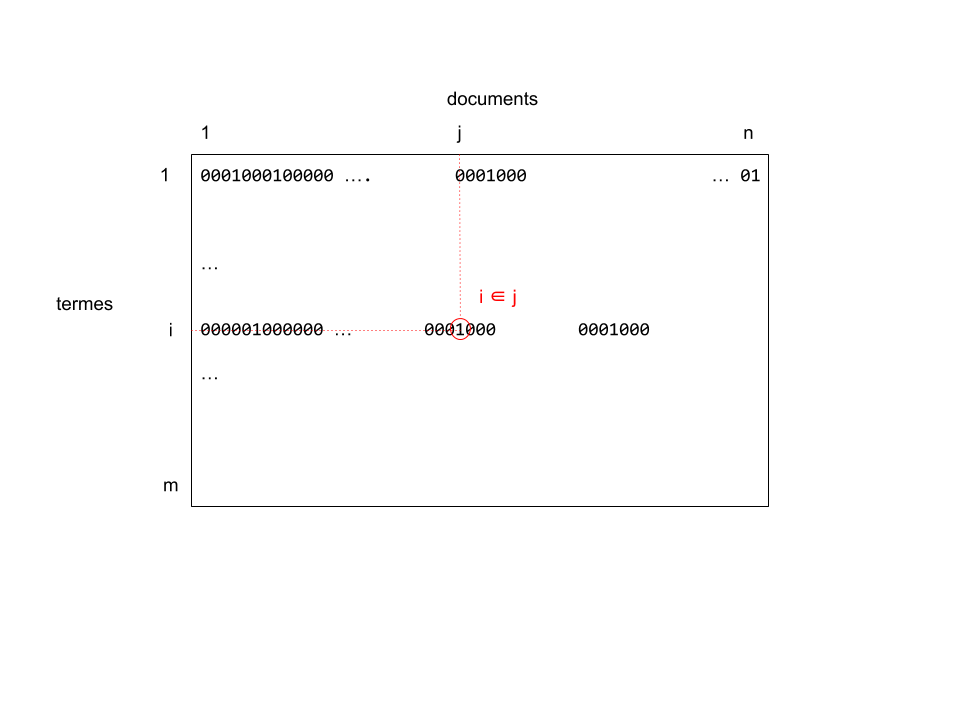
La structure de données implémentant les fichiers inverse est un tableau bidimensionnel binaire $T$ (appelé "bitmap")

$B$ est la base documentaire, de taille $n$
A chaque document $d \in B$ est attribué un entier $j \in 1..n$
$V$ est le vocabulaire, de taille $m$
A chaque terme $t \in V$ est attribué un entier $i \in 1..m$
$T[i,j] = 1 \Leftrightarrow t \in d$
$T[i,j] = 0 \Leftrightarrow t \notin d$
Chaque colonne T[:,j] désigne l'ensemble des termes contenus dans le document $d$
Chaque ligne T[i,:] désigne l'ensemble des documents contenant le terme $t$

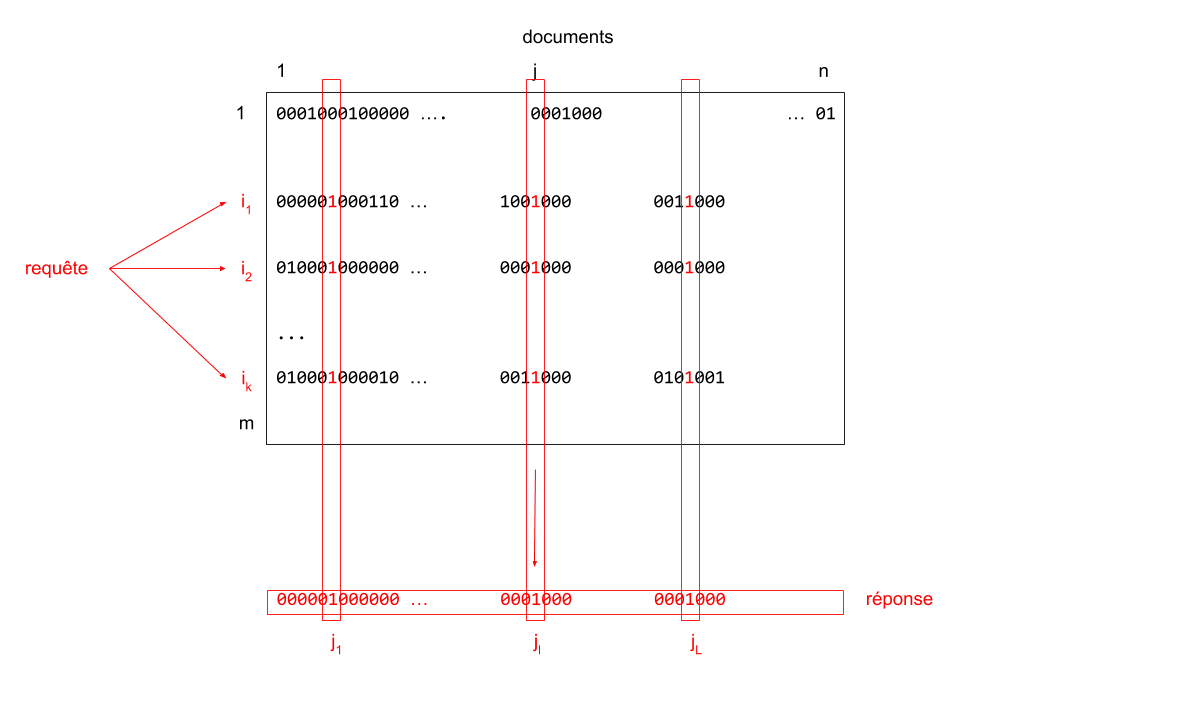
Soit $q$ une requête constituée de plusieurs termes $i_1, i_2, ... i_k$ .

Cette requête s'interprète comme la recherche des documents contenant à la fois les termes $i_1$ et $i_2, ...$ et $i_k$ .

L'ensemble des documents sélectionnés par la requête est donnée par l'opérateur booléen "and": $T[i_1, :] \text{ and } T[i_2, :] \text{ and }...\text{ and } T[i_k,:]$

Opérateur booléen appliqué sur les lignes de la matrice

On note $\{j_1, j_2, ...\}$ la liste des références des documents sélectionnés par la requête $q$ .

Parallélisation

Remarques :

On a une structure de matrice creuse (beaucoup de 0, peu de 1)
En ordre de grandeur, on a $m$ « $n$ . Typiquement $m = O(10^4), n = O(10^8)$ .

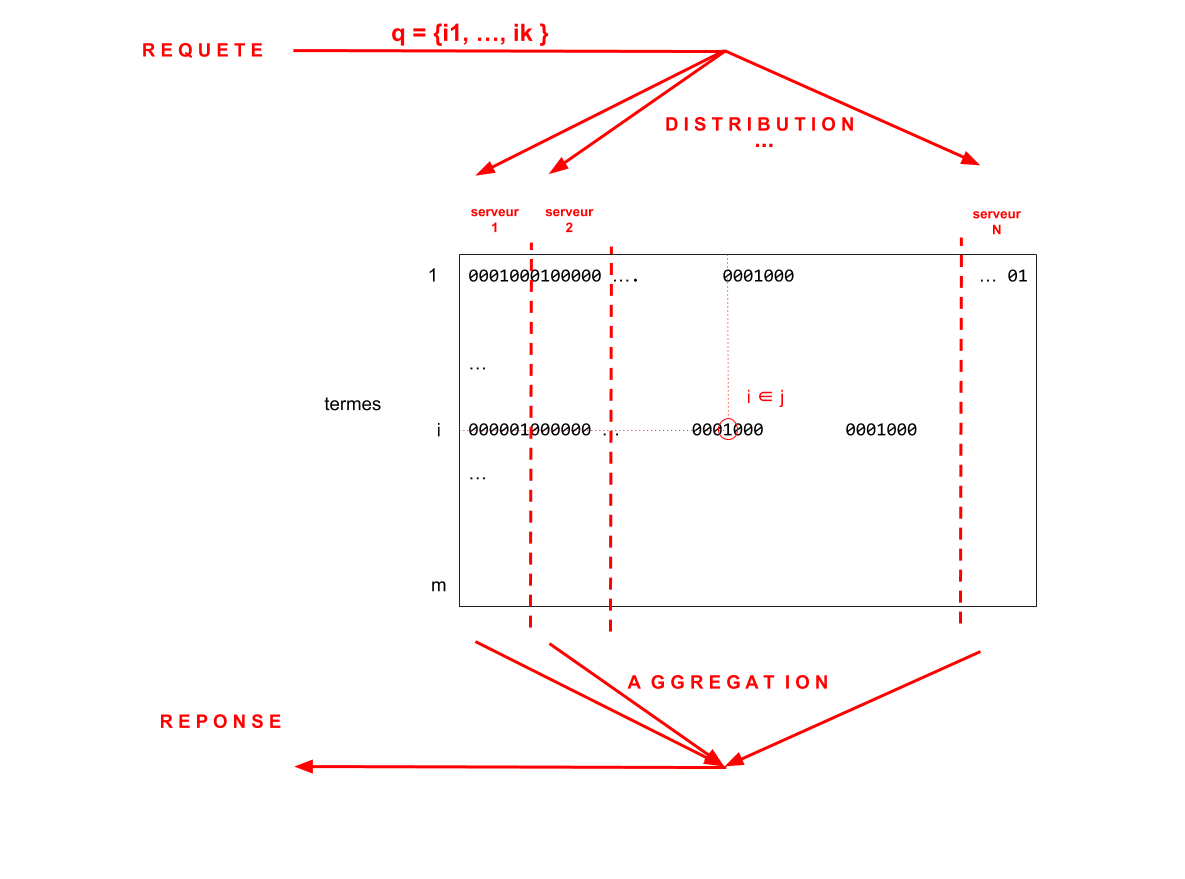
Pour réduire les temps de réponse,il est nécessaire de paralléliser les calculs en répartissant la requête sur différents serveurs.

La même requête est distribuée à différents serveurs
Chaque serveur gère un index bitmap différent (même vocabulaire / références différentes)
Chaque serveur retourne une liste de références
L'ensemble des listes est fusionnées (aggrégation des réponses)

Algorithme de référence pour la parallélisation: MAP-REDUCE .

4.2 Similarité

Pour chaque document $d$ (indexé par $j$ ) sélectionné par fichier inverse, on calcule un score de similarité : $\textbf{sim}(j,q)$

Les documents sont ensuite classés par ordre décroissant de score. La réponse est une liste ordonnée de documents : $(j_1', j_2', ...)$ avec $\text{sim}(j_1',q) \geq \text {sim}(j_2',q) \geq ...$

Représentation vectorielle des documents

Un document $d$ (indexé par $j$ ) et une requête $q$ peuvent être représentés par un vecteur binaire $\boldsymbol{x}$ de dimension $m$
- $m$ est la taille du vocabulaire
- Chaque terme $t \in V$ est indexé par un entier $i \in 1..m$
- $x_i = 1 \Leftrightarrow i \in d$
- $x_i = 0 \Leftrightarrow i \notin d$

NB Pour les documents, ce vecteur binaire est une colonne de l'index bitmap.

Similarité de Jaccard :

$\text{sim}(j,q) = \frac{ \boldsymbol{x}.\boldsymbol{q} } {||\boldsymbol{x}\oplus\boldsymbol{q}||}$

Un document $d$ (indexé par $j$ ) peut être représenté par sous la forme d'un vecteur réel $\boldsymbol{x}$ de dimension $m$
- $m$ est la taille du vocabulaire
- Chaque terme $t \in V$ est indexé par un entier $i \in 1..m$
- $x_i = w(i,d) \Leftrightarrow i \in d$
  - w(i,d) correspond :
    - à la fréquence de $i$ dans $d$ : $f(i,d)$
    - (ou) au score TF-IFD de $i$ dans $d$ : $- f(i,d) \log g(i,B)$
- $x_i = 0 \Leftrightarrow i \notin d$ $

Similarité du cosinus :

$\text{sim}(j,q) = \frac{ \boldsymbol{x}.\boldsymbol{q} } {||\boldsymbol{x}|| \times ||\boldsymbol{q}||}$

4.3 Popularité

Prise en compte de la popularité:

1ère idée : pour accélérer le tri, on établit l’ordre sur un sous-ensemble de documents présélectionnés (documents/sites les plus populaires) → priorisation dans l’ordre du calcul
2ème idée: le score de popularité peut être calculé de manière objective indépendamment des taux de fréquentation

PageRank

Le World Wide Web (www) est un réseau

formé de documents (les pages html) hébergées sur des serveurs,
les serveurs sont localisés à l'aide de leur adresse (url : universal ressource locator)
les documents sont liés entre eux par des liens hypertextes.

Les algorithmes d'indexation utilisés par les principaux moteurs de recherche prennent en compte la popularité des différentes pages~; les pages les plus "populaires" reçoivent un score plus élevé qui a tendance à les faire apparaître en premier dans la liste des réponses, selon:

$\text{score}(j,q) = \text{PR}(j) \times \text{sim}(j,q)$ où

$\text{PR}(j)$ est la popularité de la page

$j$ .

Le score de popularité le plus célèbre est le "Page Rank", proposé par Larry Page, co-fondateurs de Google.

Le calcul du Page Rank repose sur un modèle de parcours aléatoire de graphes. On considère un internaute se déplaçant sur le Web de manière aléatoire. A chaque page visitée, il suit un lien au hasard et répète cette opération un nombre indéfini de fois. Le résultat est un chemin aléatoire sur le graphe. Au cours de ce parcours, certains sites seront visités plus souvent que d'autres car il y a en moyenne plus de chemins qui y conduisent.

Modélisation statistique d’un parcours aléatoire du graphe du web

Soit un agent qui surfe sur le web au hasard

dans q% des cas il suit d’un lien du site courant au hasard (q ≃ 80%)
dans (1-q)% des cas il visite une page quelconque du réseau sans suivre de lien particulier.

q est appelé le terme d'amortissement, fixé en pratique à 0.85.

Le graphe du web est constitué de $n$ nœuds où chaque nœud est une page web. On considère que chaque page est indexée par un indice $i \in 1..n$ .

Dans ce cas, le graphe peut être représenté par une matrice

$G$ de taille

$n \times n$ contenant des 1 et de 0, telle que la valeur 1 signale la présence d'un lien et la valeur 0 l'absence de lien.

$G$ a une structure de matrice creuse (beaucoup de 0, peu de 1)

$G = \left( \begin{array}{ccccccccccc} 1& & & & & & & & & & \\ &1&1& & & & & & & & \\ &1&1& & & & & & & & \\ 1&1& &1& & & & & & & \\ &1& &1&1&1& & & & & \\ &1& & &1&1& & & & & \\ &1& & &1& &1& & & & \\ &1& & &1& & &1& & & \\ &1& & &1& & & &1& & \\ & & & &1& & & & &1& \\ & & & &1& & & & & &1\\ \end{array} \right)$ (La valeur 0 n'est pas représentée)

On peut de même définir une matrice de transition

$P$ contenant les probabilités de transition d'une page à l'autre.

$P = \left( \begin{array}{ccccccccccc} 1& & & & & & & & & & \\ &\frac{1}{2}&\frac{1}{2}& & & & & & & & \\ &\frac{1}{2}&\frac{1}{2}& & & & & & & & \\ \frac{1}{3}&\frac{1}{3}& &\frac{1}{3}& & & & & & & \\ &\frac{1}{4}& &\frac{1}{4}&\frac{1}{4}&\frac{1}{4}& & & & & \\ &\frac{1}{3}& & &\frac{1}{3}&\frac{1}{3}& & & & & \\ &\frac{1}{3}& & &\frac{1}{3}& &\frac{1}{3}& & & & \\ &\frac{1}{3}& & &\frac{1}{3}& & &\frac{1}{3}& & & \\ &\frac{1}{3}& & &\frac{1}{3}& & & &\frac{1}{3}& & \\ & & & &\frac{1}{2}& & & & &\frac{1}{2}& \\ & & & &\frac{1}{2}& & & & & &\frac{1}{2}\\ \end{array} \right)$

Le calcul du page Rank est fondé sur une estimation de la proportion de temps passée sur chaque site en suivant ce principe.

Il correspond à la mesure stationnaire de la chaîne de Markov associée, définie comme le vecteur $\boldsymbol{x}$ positif et de somme 1 vérifiant~: $\boldsymbol{x} = \boldsymbol{x}Q^T$ avec~ $Q = qP + \frac{(1-q)}{n} \boldsymbol{1}$ avec $\mathbf{1}$ matrice de taille $n \times n$ ne contenant que des 1.

En pratique :

Le graphe étant de grande taille, il n'est pas possible de résoudre directement l'équation de récurrence
Le graphe est régulièrement mis à jour pour prendre en compte les évolution du Web et de la popularité des différentes pages.

La mise à jour du graphe et du PageRank se fait de manière itérative à l'aide d'un "robot" qui parcourt le web de manière aléatoire et actualise le score de chaque page qu'il visite.

Algo :

Initialiser le vecteur $\boldsymbol{x}$ à la valeur $(1/n,1/n, ..., 1/n)$
Pour chaque page visitée $i$ :
1. Mettre à jour les valeurs des liens sortants : $\forall j : i \rightarrow j, P_{ij} \leftarrow \frac{1}{\sum_{j : i \rightarrow j}1}$
2. choisir une page $j$ au hasard parmi les liens sortants
3. Mettre à jour le score $x_j$ de la page $j$ en fonction des liens entrants, i.e. $x_j \leftarrow q \sum_{i:i\rightarrow j} P_{ij} x_i + \frac{1-q}{n}$

La popularité du site

$j$ est le logarithme en base 10 de la mesure invariante amortie de la chaîne de Markov du web (+ une constante), soit:

si $\boldsymbol{x} \in \mathbb{R}^n$ est la mesure invariante
$\text{PR}(j) = C + \log_{10} x_j$
en pratique, $C \simeq 10$

Limites :

il y a des sites qui apparaissent et qui disparaissent
les sites non référencés par le graphe principal peuvent ne jamais être vus (dark web)
l’algo a intérêt à visiter uniformément tous les sites référencés (pas seulement les plus populaires)

Abus de pageRank:

Certaines entreprises se sont spécialisées dans l'optimisation des scores de popularité (car valeur économique) à l'aide de "fermes à liens" –> séries de sites virtuels envoyant des liens vers les sites ciblés. (technique devenue obsolète avec les dernières versions de l'algorithme de Google…)

Conclusion : Des algorithmes de recherche facilement parallélisables : plus il y a de serveurs en parallèle, plus le temps de réponse est court… Une efficacité qui explique leur grand succès économique.