Table des matières
5. Classification et partitionnement
5.1 Performance de la recherche d'informations
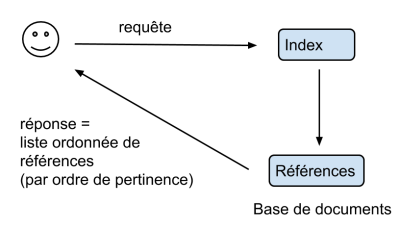
$\rightarrow$ La réponse de l’algorithme est une liste ordonnée de références, classée d’après la pertinence des résultats (≃ similarité)
On cherche à évaluer les performances d’un programme de recherche d’information. Pour ce faire, on le teste sur une base constituée de questions et de réponses (connues).
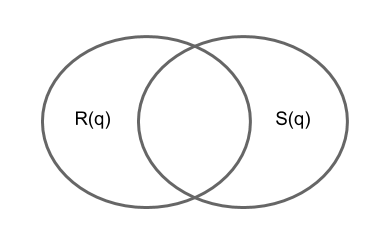
- on note $R(q)$ la liste des réponses du programme
- et $S(q)$ la liste des réponses souhaitées (“solution”).
On veut savoir : - si les réponses obtenues sont correctes? - si toutes les réponses souhaitées ont été obtenues?
Exemple:
- s'il trouve bien les mammifères?
- s'il trouve tous les mammifères?
- $ A = |R(q)|$ est le nombre total de réponses fournies par le programme (pour la requête q).
- $ B = |S(q)|$ est le nombre total de réponses souhaitées (pour la requête q).
- $C = |R(q)∩ S(q)|$ indique combien de “bonnes” réponses ont été fournies par le programme.
- $D = A - C$ indique combien de “mauvaises” réponses ont été fournies par le programme. Ce sont les faux positifs.
- $E = B - C$ indique combien de “bonnes” réponses ont été oubliées. Ce sont les faux négatifs.
Il n’y a pas de formule unique pour évaluer la performance du programme!!
- Soit $D/A$ le taux d’erreur.
- La précision du programme de recherche d'informations vaut
$$F = 1 - D/A $$
Remarques :
- La précision vaut 1 s’il n’y a pas de mauvaise reponse.
- Remarque: la précision risque de bien noter un programme qui ne donne pas assez de bonnes réponses (même si rien n’est faux dans les réponses du programme). Ce son les faux négatifs.
- Soit $E/B$ le taux d’oubli
- Le rappel du programme de recherche d'informations vaut
$$G = 1 - E/B$$
Remarques :
- Le rappel vaut 1 lorsqu'on n’a pas oublié de bonne réponse.
- Il vaut 1 si toutes les bonnes réponses y sont.
- Néanmoins, le rappel risque de bien noter un programme qui donne trop de réponses (meme si toutes les bonnes réponses y sont). Ce sont les faux positifs.
Conclusion : pour mesurer la performance du programme, il faut considérer deux notes et non pas une seule. La performance d’un programme se mesure sur un axe (précision, rappel).
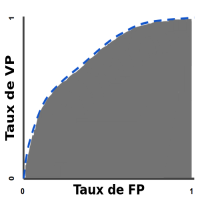
Une courbe ROC (receiver operating characteristic) est un graphique représentant les performances d'un modèle de classification pour tous les seuils de classification. Cette courbe trace le taux de vrais positifs en fonction du taux de faux positifs :
Une courbe ROC trace les valeurs TVP et TFP pour différents seuils de classification. Diminuer la valeur du seuil de classification permet de classer plus d'éléments comme positifs, ce qui augmente le nombre de faux positifs et de vrais positifs. La figure ci-dessous représente une courbe ROC classique.
5.2 Classification de documents
Exemples de tâches de classification:
- Partitionnement. On a une base de documents non classés. On veut construire des classes regroupant les documents qui se “ressemblent” le plus.
- Identification (reconnaissance). On a une base de documents classés. On veut trouver la classe d’un document $d$ inconnu.
Principe de mise en oeuvre
Mesures de similarité. On utilise une des mesures de similarité vues précédemment et "groupe" ensemble les documents qui se ressemblent.
Bases d'exemples. Une base d'exemples est un ensemble de couples $\{(d_1,r_1),...,(d_n,r_n)\}$ constitué de $n$ documents étiquetés, où les $d_i$ sont les documents et les $r_i$ sont les réponses attendues.
Soit $P$ un programme de recherche d'informations. Les bases d'exemples permettent de produire une estimation des taux de bonne réponses et des taux d'erreurs produits par le programme.
Remarque: les réponses peuvent être simples ou multiples, c'est à dire qu'un document peut appartenir à une catégorie unique ou au contraire appartenir à de nombreuses catégories.
Soit $C$ un ensemble de catégories. Pour un ensemble d'exemples donnés, on mesure les performances d'un programme de classification à l'aide d'une matrice de confusion:
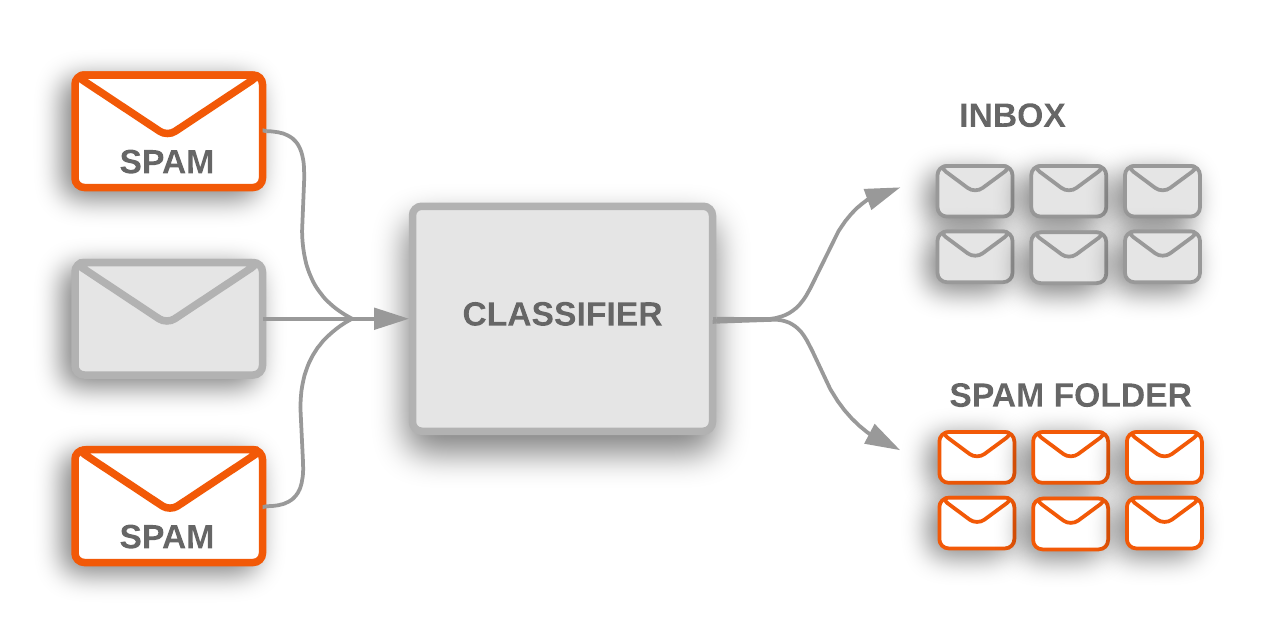
Exemple: On souhaite mesurer la qualité d'un système de classification de courriers électroniques. Les courriers sont classifiés selon deux classes : courriel pertinent ou pourriel intempestif. Supposons que notre classificateur est testé avec un jeu de 200 mails, dont 100 sont des courriels pertinents et les 100 autres sont des pourriels.
Pour cela, on veut savoir :
- combien de courriels seront faussement estimés comme des pourriels (fausses alarmes) et
- combien de pourriels ne seront pas estimés comme tels (non détections) et classifiés à tort comme courriels.
| Classe estimée par le classifieur | Courriel | Pourriel | |
|---|---|---|---|
| Classe réelle | Courriel | 95 (vrais positifs) | 5 (faux positifs) |
| Pourriel | 3 (faux positifs) | 97 (vrais négatifs) | |
La matrice de confusion suivante se lit alors comme suit :
- horizontalement, sur les 100 courriels initiaux (ie : 95+5), 95 ont été estimés par le système de classification comme tels et 5 ont été estimés comme pourriels (ie : 5 faux-négatifs),
- horizontalement, sur les 100 pourriels initiaux (ie : 3+97), 3 ont été estimés comme courriels (ie : 3 faux-positifs) et 97 ont été estimés comme pourriels,
- verticalement, sur les 98 mails (ie : 95+3) estimés par le système comme courriels, 3 sont en fait des pourriels,
- verticalement, sur les 102 mails (ie : 5+97) estimés par le système comme pourriels, 5 sont en fait des courriels.
- diagonalement (du haut gauche , au bas droit), sur les 200 courriels initiaux, 192 (95 + 97) ont été estimés correctement par le système.
Méthode K plus proches voisins
La méthode des K plus proche voisins permet de prédire la classe d'un document $d$ inconnu à partir des classes des documents les plus similaires au document courant.
La liste des voisins est obtenues par calcul de similarité entre le document courant et l'ensemble des exemples de la base. Une fois les valeurs de similarité calculées, on sélectionne les $K$ documents qui donnent le score de similarité le plus élevé.
- Il est possible de tester plusieurs valeurs de $K$ et de choisir celle qui donne le meilleur taux de classification.
- La méthode la plus simple consiste à prendre $K=1$, c'est à dire qu'on attribue la classe du document qui ressemble le plus au document inconnu.
- Plus $K$ est élevé, plus la méthode sera robuste aux erreurs de classification.
Une fois la liste des voisins déterminée, il faut déterminer la classe du document:
- Méthode du vote majoritaire. La fonction retourne la classe la plus probable par vote majoritaire (chaque voisin vote pour sa classe).
- Moyenne pondérée. Chaque classe $c$ se voit attribuer un score $w_c$:
$$ w_c = \frac{\sum_{v \in \text{Voisins}; c \in r(v)}sim(d,v)}{\sum_{v \in \text{Voisins}}sim(d,v)}$$ La fonction retourne la classe au score le plus élevé.
Régression logistique
voir : calculating-a-probability
Classifieur Bayésien
Un classifieur bayésien estime la probabilité d'appartenance d'un document $d$ à la classe $c$. Grâce à cette probabilité, il est possible de retourner la classe la plus probable, mais également la probabilité d'erreur de classification pour chaque réponse produite.
Soit $V$ un vocabulaire de taille $m$. Soit $t$ un terme de vocabulaire. On note $p(t|c)$ la probabilité que le terme $t$ apparaisse dans un document de classe $c$.
On suppose qu'il existe pour chaque terme une probabilité conditionnelle associée à la classe, appelée la vraisemblance (vraisemblance du fait que le terme $t$ apparaisse dans le document s'il est de classe $c$.)
La formule de Bayes permet de dire, étant donnée l'observation du terme $t$, la probabilité inverse (dite postérieure), c'est à dire la probabilité de la classe $c$ conditionnée à $t$.
$$p(c|t) = \frac{p(t|c) p(c)}{\sum_{c' \in C} p(t|c') p(c')}$$
Si $d$ est un document contenant $k$ termes $t_1, ..., t_k$, la formule se généralise à : $$p(c|t_1,...,t_k) = \frac{p(t_1,...,t_k|c) p(c)}{\sum_{c' \in C} p(t_1,...,t_k|c') p(c')}$$
En général, on ne dispose pas des probabilités $p(t_1,...,t_k|c)$. On utilise en général l'approximation, dite du Bayes naïf: $$p(d|c) \simeq p(t_1,...,t_k|c) \simeq p(t_1|c) \times ... \times p(t_k|c)$$
Au final, la réponse du classifieur repose sur un produit de probabilités élémentaires portant sur les fréquences documentaires des termes présents dans les groupes de documents appartenant à certaines classes.
Pour construire le classifieur:
- La base d'exemples est partitionnée en sous-bases, selon les classes
- pour chaque sous-base, on calcule la fréquence documentaire de chaque terme de vocabulaire
Pour classer un document $d$ inconnu, le classifieur retourne la classe qui maximise le score de vraisemblance, soit : $$ \max_c g(t_1,c) \times ... \times g(t_k,c)$$
Partitionnement
Il existe deux grandes méthodes de partitionnement :
- L'algorithme des K-moyennes