tc_info:2020_cm

−Table des matières

Bases de données relationnelles

Bases de données relationnelles

On introduit dans ce chapitre le modèle relationnel qui sert de fondation à la conception de bases de données.

Les différents modèles utiles en représentation des connaissances reposent sur des notions de base de la théorie des ensembles :

Ensemble finis
Éléments partiellement (ou totalement) discernables

1 Structures de données

1.1 Production des données

Tout commence par une fiche à remplir…

Un formulaire se présentant sous la forme d’un ensemble de rubriques à remplir.
Le modèle de fiche définit le format des données à enregistrer:
- liste des rubriques du formulaire,
- domaine de valeurs attendues dans chaque rubrique.
A toute fiche remplie correspond un jeu de valeurs (ou mesure) :
- liste de valeurs correspondant au contenu d’une fiche particulière.

Un jeu de valeurs sert à décrire :

une personne réelle : assuré, client, étudiant, auteur, plaignant, contribuable,…
une personne morale : fournisseur, prestataire, direction, section, promotion,…
un objet physique : article, véhicule, composant, ingrédient, pièce,…
un objet contractuel ou administratif : fiche de paye, contrat, procès verbal, billet, dossier…
un lieu : salle, local, manufacture, entrepôt, ligne de production,…
un événement : transaction, jugement, achat, vente, acte administratif, appel téléphonique,…
etc…

1.2 Stockage des données

D’un point de vue informatique, un jeu de valeurs recueilli est appelé un enregistrement
- correspondant à l’encodage des données recueillies sur un support numérique
Une structure de données définit les données de manière logique,
- c’est à dire l’ordre dans lequel elles doivent être lues
- et la manière dont elles doivent être interprétées par les programmes qui les utilisent.

Exemples de structures de données (cours d'algorithmie):

listes,
listes de listes,
dictionnaires,
arbres,…

Les types des valeurs étant déterminés (selon les cas de taille fixe ou variable),
- la structure de données correspond au “véhicule” qui servira à transporter et échanger les données (entre programmes, entre ordinateurs).
- Différentes structures de données sont possibles pour l’encodage et le stockage d’un jeu de valeurs, voir :
  - Données non structurées
  - Données vectorielles
  - Tuples
  - Données structurées
  - Données Hiérarchisées

Tuples

Le Tuple est la structure de données de base servant pour le recueil, le transport et le stockage des données.

Un Tuple est une liste, finie, ordonnée et de taille fixe contenant une suite de valeurs.
Chaque valeur peut obéir à un format différent
On note m la taille du tuple (nombre de valeurs)

$t = (a_1, ..., a_m)$ Exemple :

("Dubois", "Martine", 22, "29/10/1994", "Orléans")

NB: un tuple est une séquence (ordonnée et finie) de valeurs, chaque valeur pouvant être de type qualitatif ou quantitatif, et pouvant obéir à un format numérique différent.

Exemple : considérons une fiche servant à décrire un étudiant. L’étudiant doit remplir les rubriques nom, prénom et âge, numero de voie, nom de la voie, code postal, ville. Chaque rubrique correspond à un composant d’un 7-tuplet tel que:

les composants 1, 2, 5 et 7 sont des chaînes de caractères
les composants 3, 4 et 6 sont des entiers

Le format csv - “Comma Separated Values”

Chaque enregistrement est codé sur une ligne, chaque valeur étant séparé par un caractère séparateur (virgule, point-virgule, tabulation,…).

Exemple :

Dubois,Martine,"28, rue des Lilas, 45000 Orléans",45

Remarques :

les données sont des chaînes de caractères
les guillemets sont nécessaires lorsque la valeur contient le caractère séparateur (ici la virgule)
les noms des attributs sont éventuellement indiqué sur une ligne séparée

Données indexées

Données organisées sous la forme d’une liste d’attributs.
- Chaque attribut est défini par un nom et un format (type).
- Chaque valeur est stockée sous la forme d’un couple (attribut : valeur).

Exemple :

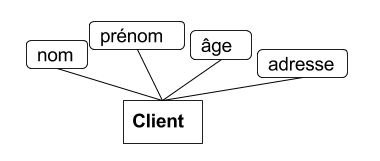
Considérons une fiche servant à décrire un étudiant. L’étudiant doit remplir les rubriques nom, prénom et âge, numero de voie, nom de la voie, code postal, ville.

Chaque rubrique correspond à un attribut, où:

nom, prenom, voie, et ville sont des attributs de type chaîne de caractères
age et numero et code_postal sont des attributs de type entier

La structure de données sous-jacente est le dictionnaire, où l’attribut est la clé permettant d’accéder à la valeur.

Un dictionnaire est une liste non ordonnée de valeurs, chaque valeur étant associée à une clé unique (ici la clé est le nom de l’attribut).

Le format json - JavaScript Object Notation

Exemple :

{"nom" : "Dubois", "prénom" : "Martine", "adresse" : "28, rue des Lilas, 45000, Orléans", "âge" : 45}

Remarques :

reprend la syntaxe vue en Python
données numériques ou chaînes de caractères

Données Hiérarchisées

Organisation des données correspondant à une structure d’arbre.
Dans le cas d’un recueil de données, correspond à la définition de rubriques et sous-rubriques.

Exemples :

La rubrique adresse peut contenir les sous-rubriques numero, voie, code_postal et ville.
Un document contient des chapitres, des sections, des sous-sections etc…

Formats xml, xhtml, json, …

Pour les données organisées de manière hiérarchique. Des balises servent à séparer les différents attributs.

Ex :

<nom> Dubois </nom>
<prénom> Martine </prénom>
<adresse>
  <num> 28 </num>
  <voie> rue des Lilas </voie>
  <code postal> 45000 </code postal>
  <ville> Orléans </ville>
</adresse>
<âge> 45 </âge>

remarque : le format json permet également de définir des hiérarchies

{
  "nom" : "Dubois",
  "prénom" : "Martine",
  "adresse" :
  {
    "numero" : 28,
    "voie" : "rue des Lilas",
    "code_postal" : 45000,
    "ville" : "Orléans"
  },
  "âge" : 45
}

Tableaux de données

Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$ .

2. Schéma et relation

2 approches en modélisation :

approche ensembliste (plus général)
modèle relationnel (plus pratique)

Le Modèle relationnel sert à représenter logiquement les tableaux de données.

Tableau de données

Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$ .

Rappel:

Un enregistrement est un jeu de valeurs organisé sous forme de tuple
A un tuple on associe en général un schéma de données.

Définir un schéma consiste à définir :
- une liste d'attributs (labels) associées à chacune des valeurs du tuples.
A chaque attribut correspond :
- un intitulé
- un domaine de valeurs (type/format des données)

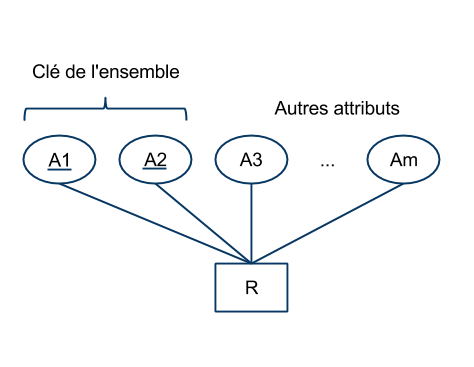
Soit $R(A_1, ..., A_m)$ un schéma.
On note $\text{dom}(A_i)$ le domaine associé à l'attribut $A_i$ .
On dit d'un tuple $t$ qu'il obéit au schéma $R$ si les valeurs qu'il contient correspondent aux domaines des attributs du schéma.

Définition

Soit $R = (A_1,...,A_m)$ un schéma de données

Une relation $r$ obéissant au schéma $R$ est un sous-ensemble du produit cartésien $\text{dom}(A_1) \times ... \times \text{dom}(A_m)$

Corollaire : une relation est un ensemble de tuples :

$r = \{t_1, ..., t_n\} = \{ (a_{11}, ..., a_{1m}), ..., (a_{n1}, ..., a_{nm})\}$

avec :
- $\forall (i,j), a_{ij} \in \text{dom}(A_j),$
- $\forall i, t_i \in \text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- $n$ : nombre de tuples
- $m$ : nombre d'attributs par tuple

Remarque :

Le schéma $R$ représente le niveau abstrait (modélisation)
La relation $r$ représente un cas concret de réalisaton (à un schéma $R$ peuvent correspondre une infinité de réalisations possibles : $r$ , $r'$ , $r''$ , etc. )

Diverses représentations :

Entité/association :

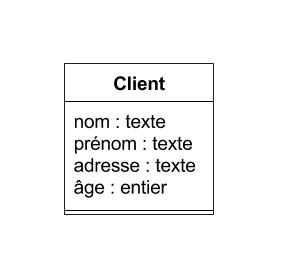
UML :

Schéma relationnel :

Client(nom, prénom, adresse, âge)

Exemples de schémas relationnels :

Étudiant(nom, prénom, adresse, INE)

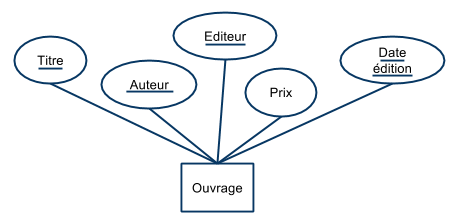
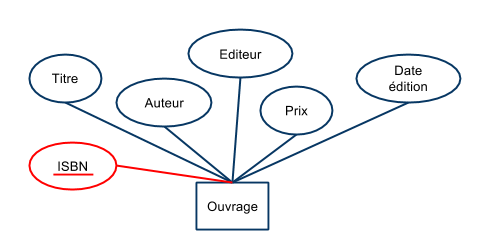
Ouvrage(titre, auteur, éditeur, prix, date_édition)

Véhicule(immatriculation, marque, modèle, couleur)

3. Dépendances fonctionnelles

Au sein d'un schéma $R$ ,
- Il peut exister un ensemble de contraintes, noté $F$ ,
  - portant sur les attributs (plus précisément sur les valeurs prises par les attributs).
  - L'ensemble F est indépendant de R.
- On parle de contraintes d’intégrité.
  - Ces contraintes s’expriment sous la forme de dépendances fonctionnelles.

Rappels d’algèbre de base:

Relation binaire : une relation binaire $r$ portant sur deux domaines $\text{dom}(A)$ et $\text{dom}(B)$ :
- est un sous-ensemble du produit cartésien $\text{dom}(A) \times \text{dom}(B)$ .
- si $(a,b) \in r$ , on note parfois $a r b$ ce qui signifie “a est en relation avec b”.
Fonction : une fonction $f : \text{dom}(A) \rightarrow \text{dom}(B)$ est une relation binaire sur $\text{dom}(A) \times \text{dom}(B)$ telle que
- pour tout $a \in \text{dom}(A)$ ,
- il existe un unique $b$ tel que $(a,b) \in f$ .
- On note $b=f(a)$ ,
  - ce qui signifie qu'au sein de la relation $f$ , $b$ est déterminé de façon unique par le choix de $a$ (autrement dit : “b dépend de a”)

Dépendance fonctionnelle

Soit $r$ une relation définie selon $R(A_1,...,A_m)$
Soient $X$ et $Y$ deux sous-ensembles de $R$
On dit que la relation $r$ définit une dépendance fonctionnelle de $X$ vers $Y$ ,
- notée $X \stackrel{r}{\rightarrow} Y$
- si les valeurs de $r$ permettent de définir une fonction de $\text{dom}(X)$ vers $\text{dom}(Y)$ .

Exemple 1 :

Soit la relation $r$ :

A	B	C
1	a	e
2	b	f
2	c	f
3	d	k
4	d	k

On a les dépendances suivantes :
- $A \rightarrow C$
- $B \rightarrow C$
- mais pas : $A \rightarrow B$ , $B \rightarrow A$ , ni $C \rightarrow A$
On a aussi :
- $A,B \rightarrow C$
- mais pas : $B,C \rightarrow A$ , ni $A,C \rightarrow B$ , etc.

Exemple 2 :

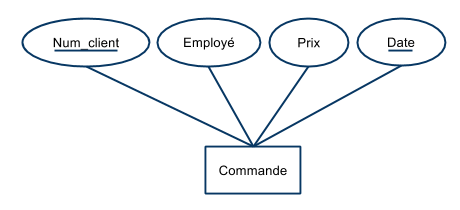
Soit le schéma :
- Commande (num_client, quantité, prix, date, num_article)
et l’ensemble de contraintes

$\begin{array}{rl}F &= \{\\ & \text{num_client, date} \rightarrow \text{num_article, quantité, prix} \\ & \text{num_article, quantité} \rightarrow \text{prix} \\ &\} \end{array}$

La première contrainte indique qu'il ne peut y avoir deux factures émises pour un même client à une date donnée.
La seconde contrainte indique que le prix payé dépend de l’article et de la quantité commandée.

Exemple 3 :

Soit le schéma :
- Ouvrage (titre, auteur, éditeur, prix, date_edition)
et la contrainte :
- {titre, auteur, éditeur → prix, date_édition}

La contrainte signifie :

“pour une oeuvre chez un certain éditeur, une seule édition est possible (pas de réédition à une date ultérieure)”
“politique du prix unique”

Exercice : Soit le schéma :

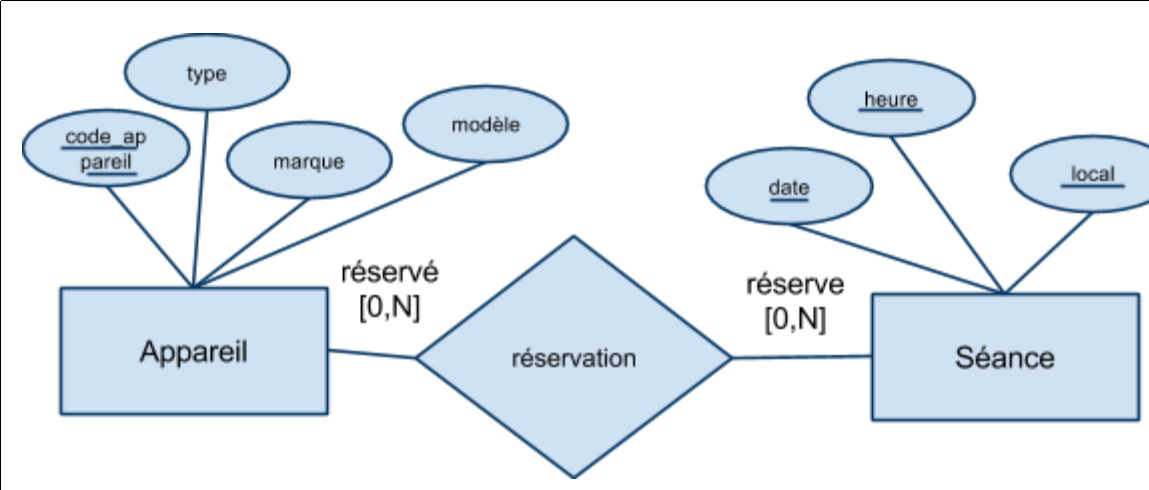
Réservation(code_appareil, date, heure, salle)

Exprimer la dépendance fonctionnelle :

« Un appareil ne peut pas être utilisé dans deux locaux différents au même moment »

Il importe donc de bien réfléchir, au moment de l'étape de conception,
- du réalisme et du caractère limitant de certaines dépendances fonctionnelles,
- et du caractère éventuellement limitant du choix des attributs.
Ainsi, le schéma décrivant les commandes (exemple 2)
- ne permet pas de commander des articles de nature différente au sein d'une même commande
- (un client, pour commander deux râteaux et une truelle, doit donc effectuer deux commandes, qui plus est à des dates différentes!).

Exercice

Soit le schéma relationnel suivant :

Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)

Définir des dépendances fonctionnelles sur cet ensemble d'attributs

4. Clé d'une relation

4.1 Définitions

Soit un schéma $R(A_1, ..., A_m)$ .

Clé

Une clé $K$ :
- est un ensemble minimal d'attributs inclus dans R,
- tel que toute relation $r$ de schéma $R$ définit une dépendance fonctionnelle de $dom(K)$ dans $dom(R)$ ,
cette dépendance est notée $K \rightarrow R$ .

Remarques :
- Si un schéma $R$ possède une clé $K$ , alors tous les éléments d’une relation $r$ de schéma $R$ sont discernables : la valeur de la clé permet d’identifier de façon unique chaque élément de l’ensemble.
- Au sein d'un schéma, il est souvent possible de définir plusieurs clés à partir des attributs. Le concepteur du modèle choisit une clé parmi les clés possibles. Cette clé est appelée clé primaire.
- Graphiquement, les attributs constituant la clé sont soulignés:

Exemple 1 :

Exemple 2 :

Pour certains schémas,
- il est courant de définir comme clé un entier identifiant de façon unique chaque élément de l'ensemble (appelé identifiant ou “Id”).
- La clé est alors constituée de cet attribut unique.

Représentation UML :

4.2 Axiomes d'Amstrong

Soit $K$ une clé candidate. On démontre que $K \rightarrow R$ à l'aide des axiomes d'Amstrong à partir d'un ensemble de DF connues:

Axiomes d'Amstrong

Réflexivité : $Y \subseteq X \Rightarrow X \rightarrow Y$
Augmentation : $X \rightarrow Y \Rightarrow X,Z \rightarrow Y,Z$
Transitivité : $X \rightarrow Y \text{ et } Y \rightarrow Z \Rightarrow X \rightarrow Z$
Pseudo-transitivité : $X \rightarrow Y \text{ et } Y,W \rightarrow Z \Rightarrow X,W \rightarrow Z$
Union : $X \rightarrow Y \text{ et } X \rightarrow Z \Rightarrow X \rightarrow Y,Z$
Décomposition : $X \rightarrow Y, Z \Rightarrow X \rightarrow Y \text{ et } X -> Z$

Exercice

Soit le schéma relationnel suivant :

Montrer que l'ensemble {num_train, num_voiture, num_place, date, gare_départ} est une clé primaire du schéma?

4. Normalisation d'un schéma

Tables mal construites

Exemple : fournisseurs de composants électroniques:

$\textbf{Fournisseur}(\underline{\text{nom_f, composant}}, \text{adresse_f, prix})$

Problèmes :
- Redondance : l’adresse des fournisseurs est répétée plusieurs fois
- Inconsistance : mauvaise mise à jour ⇒ adresses différentes pour un même fournisseur.
- Problème Insertion : on ne peut pas insérer dans la table un fournisseur qui ne fournit rien
- Problème suppression : si un fournisseur ne fournit plus rien, on perd son adresse
Solution?

Couper la table en 2?

$\textbf{Fournisseurs} (\text{nom_f, adresse_f})$

$\textbf{Catalogue}(\text{composant, prix})$

–> Impossible de retrouver les prix pratiqués par les différents fournisseurs.

Nouveau Schéma :

$\textbf{Fournisseurs} (\text{nom_f, adresse_f})$

$\textbf{Catalogue}(\text{nom_f, composant, prix})$

–> Il est possible de reconstruire la table initiale en effectuant une jointure entre ces 2 tables sur l’attribut nom_f.

Exercice : Les tables suivantes sont-elles bien ou mal construites?

Enseignement (id_enseignant, nom_enseignant, matière, id_élève, nom_élève)

Arrêt (num_train, horaire, nom_gare, ville)

Facture (id_client, date, article, montant)

5. Formes Normales

Les Formes normales

Restreignent les dépendances admises dans un schéma relationnel
Permettent d’éviter la duplication de l’information au sein des relations
Définissent une méthode
- de décomposition d’un schéma relationnel redondant
- en plusieurs schémas liés entre eux:

5.1 2ème forme normale (2FN)

Dépendance fonctionnelle élémentaire (DFE)

Soit $R$ un schéma relationnel
Soit $X$ un ensemble d’attributs ⊆ $R$
Soit $A$ un attribut de $R$
Il existe une DFE entre $X$ et $A$ ssi :
- $X \rightarrow A$
- Il n’existe aucun sous-ensemble $Y$ ⊆ $X$ tel que $Y \rightarrow A$

2ème forme normale (2FN)

Un schéma $R$ est en 2FN :
- ssi la clé primaire de $R$ est en DFE avec tous les autres attributs.
- Donc : il n’y a pas d’attributs qui ne dépendent que d’une partie de la clé.

Exemple :

$\textbf{Fournisseur}(\underline{\text{nom_f}, \text{composant}}, \text{adresse_f}, \text{prix})$

$\text{nom_f} \rightarrow \text{adresse_f}$

$\text{nom_f}, \text{composant} \rightarrow \text{prix}$ ⇒ Pas 2FN!!

5.2 Normalisation 2FN

Lorsqu’un schéma relationnel n’est pas en deuxième forme normale, il doit être normalisé:

Normalisation 2FN :

Pour obtenir un schéma 2FN:
- on “découpe” la table selon les DFE trouvées entre les attributs de la clé et ceux qui ne sont pas dans la clé.
La normalisation consiste:
- à créer une nouvelle table pour chaque DFE ainsi trouvée.

Soit :

$\mathbf{R} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,\color{red}{B_j},...,B_m)$

avec :

$\color{red}{A_i} \stackrel{DFE}{\rightarrow} \color{red}{B_j}$ $A_1,...,\color{red}{A_i},...,A_n \stackrel{DFE}{\rightarrow} B_1,...,B_{j-1},B_{j+1}...,B_m$

Alors le schéma de table doit être modifié comme suit :

$\mathbf{R_1} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,B_{j-1},B_{j+1}...,B_m)$ $\mathbf{R_2} (\underline{\color{red}{A_i}},\color{red}{B_j})$

Attention

Même si aucun attribut ne dépend plus de la clé primaire initiale, il est important de la conserver dans une table spécifique (elle sert à “lier” les valeurs dispersées dans les différentes tables).

Exemple

Avant:

$\textbf{Fournisseur}(\underline{\text{nom_f,composant}}, \text{adresse_f, prix})$ $\text{nom_f} \rightarrow \text{adresse_f}$ $\text{nom_f, composant} \rightarrow \text{prix}$

Après:

$\textbf{Catalogue}(\underline{\text{nom_f,composant}}, \text{prix})$ $\textbf{Fournisseur}(\underline{\text{nom_f}}, \text{adresse_f})$

Remarque : le schéma est maintenant constitué de deux tables.

Les tables ont un attribut commun : nom_f (clé primaire de la table Fournisseur).
La clé primaire de la table des Fournisseurs est dupliquée dans la table des prix (appelée ici Catalogue).
On dit que nom_f est une clé étrangère de la table des prix (l’attribut fait référence à la clé primaire d’une autre table, en l’occurrence la table des fournisseurs - voir 3.1.1).

5.3 3ème forme normale (3FN)

Dépendance Fonctionnelle Directe (DFD) :

La dépendance fonctionnelle entre 2 attributs $A_i$ et $A_j$ est directe s’il n’existe pas de $A_k$ tel que : $A_i \rightarrow A_k \rightarrow A_j$

3ème Forme Normale (3FN)

Un schéma est 3FN :

S’il est 2FN
Si tous les attributs sont en DFD avec la clé.

Exemple :

$\textbf{Commande} (\underline{\text{num_commande}}, \text{nom_f, adresse_f, composant, quantité})$ $\text{num_commande} \rightarrow \text{nom_f, composant, quantité}$ $\text{nom_f} \rightarrow \text{adresse_f}$

Le schéma n’est pas 3FN!! (dépendance transitive entre num_commande et adresse)

5.4 Normalisation 3FN

* Lorsqu’un schéma relationnel n’est pas en troisième forme normale, il doit être normalisé:

Normalisation 3FN

On crée une table pour chaque DFD trouvée au sein des attributs n'appartenant pas à la clé.

Soit : $R (\underline{A_1,...,A_m},B_1, ..., \color{red}{B_i},...,\color{red}{B_j},...,B_n)$ avec : $A_1, ..., A_m \stackrel{DFD}{\rightarrow} B_1, ...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n$ $\color{red}{B_i} \stackrel{DFD}{\rightarrow} \color{red}{B_j}$ Alors : $R_1 (\underline{A_1,...,A_m},B_1,...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n)$ $R_2 (\underline{\color{red}{B_i}},\color{red}{B_j})$

Attention

Comme précédemment, il est important de conserver la clé primaire de la table initiale si elle permet d'associer les valeurs dispersées dans les tables.

Exemple :

Avant :

Commande (num_commande, nom_f, adresse_f, composant, quantité)
avec :
- num_commande → nom_f, composant, quantité
- nom_f → adresse_f

Après :

Commande (num_commande, nom_f, composant, quantité)
Client (nom_f, adresse_f)

L’attribut nom_f est maintenant clé primaire de la table Client et clé étrangère de la table Commande.

6. Modèle ensembliste

Pour leur conception, les bases de données sont ici vues comme des ensembles constitués de plusieurs populations d'objets en interaction, participant au bon fonctionnement d'un certain système. Établir un schéma de base de données consiste à décrire ces différentes populations d'objets, mais surtout et principalement à décrire les dépendances et les interactions entre ces populations.

Une base de donnée est constituée de plusieurs ensembles d'objets et d'opérateurs participant au bon fonctionnement d'un système:

Exemple 1 :

Ensembles d'employés
Ensembles de commandes
Ensembles d'articles
Ensembles de clients

Exemple 2 :

Ensembles d'étudiants
Ensembles de séances
Ensembles de cours
Ensembles de copies

On parle plus généralement d'ensembles d'entités.

Le modèle entité/association

Le modèle entité/associations est une méthode de description des relations entre ensembles d’entités. Il s’appuie sur le prédicat selon lequel tous les éléments des ensembles d’entités sont discernables.

Le modèle entités/associations repose sur un langage graphique de description des données, indépendant du support et de la mise en œuvre informatique.

Généralités

Une entité $x$

est une représentation d'un objet du monde réel,
appartenant au système/à l'organisation modélisée.
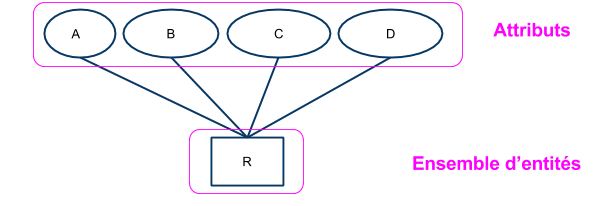
Une entité est décrite par une ou plusieurs valeurs caractéristiques, appelées attributs.

Les informations conservées au sujet des entités d'un ensemble sont les attributs.

Chaque attribut :
- a un nom unique dans le contexte de cet ensemble d'entités : $A$ , $B$ , $C$ , $A_1$ , $A_2$ , …, $A_m$ , …
  - Exemples de noms concrets : couleur, nom, horaire, salaire.
- prend ses valeurs dans un domaine bien spécifié,
  - également appelé le type de l'attribut.
  - Le domaine d'un attribut est noté $\text{dom}(Aj)= Dj$ .
    - Exemples :
      - $\text{dom}(couleur)={rouge, vert, bleu, jaune}$ ,
      - $\text{dom}(nom) =$ ensemble des chaînes de caractères,
      - $\text{dom}(salaire) =$ entiers naturels
      - etc…

Un attribut $A_j$ est une fonction à valeur sur $D_j$ :

$A_j : E \rightarrow D_j$ $x \mapsto A_j(x)$

Un attribut peut être :
- simple ou composé.
  - Exemple : une adresse peut être décrite par une simple chaîne de caractères, ou peut être décomposée en rue , no, boîte, ville, code postal, pays.
- obligatoire ou facultatif ( $D_j$ peut ou non contenir la valeur ø ).
- atomique ou non (Un attribut peut posséder 0, 1 voire plusieurs valeurs…)

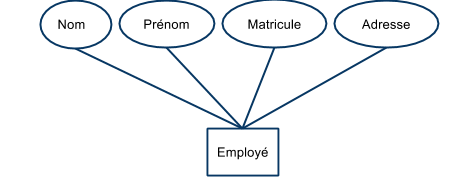
Un ensemble d'entités est un ensemble fini d'éléments : $E = \{x_1,…,x_n\}$ Il regroupe (ou associe) plusieurs entités ayant des caractéristiques communes (descriptibles à l'aide du même ensemble d'attributs).

Exemples :

les employés d'une firme,
les cours de Centrale Méditerranée,
une collection de disques,
etc…

Les éléments d’un ensemble d’entités sont partiellement discernables à travers les valeurs de leurs attributs :
- les attributs $(A_1,...,A_m)$ servent à décrire les éléments de l’ensemble.
- Le schéma $R$ de l’ensemble $E$ est une application de l'ensemble d'entités vers l'ensemble des tuples de schéma $R$
  - Soit :

$R : \mathcal{X} \rightarrow D_1 \times ... \times D_m$ $x_i \mapsto (A_1(x_i),…, A_m(x_i))$

représentation graphique :

Exemples :

Définitions

Modéliser une base de données, c'est :

Identifier les différents ensembles en interaction
Identifier les liens de dépendance entre les différents ensembles

Les liens entre les différents ensembles sont appelés des associations

Association

Une association exprime des relations de dépendance entre deux ou plusieurs ensembles d’entités.

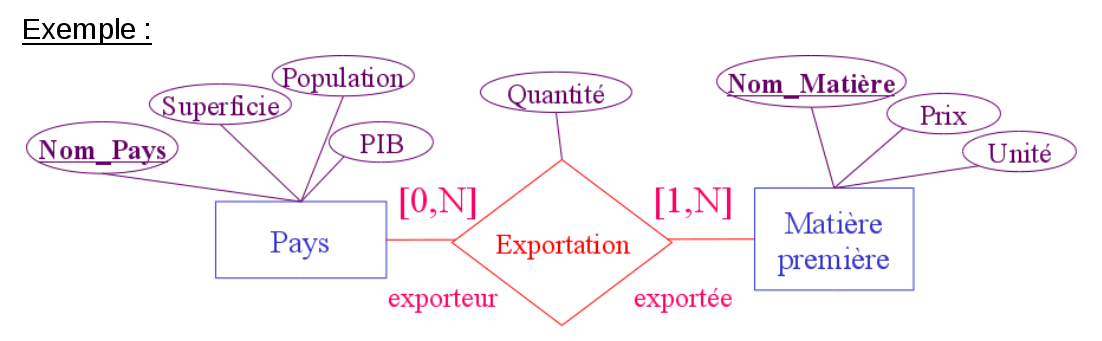
Définition : Une association entre les ensembles $E_1$ , …, $E_k$ est un sous-ensemble du produit $E_1 \times ... \times E_k$ .

Il s'agit donc d'un ensemble de k-uplets $\{..., (x_1,…,x_k), …\}$ t.q. $x_1 \in E_1,…, x_k \in E_k$ .

où $k$ est le degré de l'association :

k=2 : association binaire
k=3 : association ternaire
etc…

Rôles des associations

Attribution : propriété, réservation, participation, supervision, auteur, rôle, pilote, …
Événements : achat, vente, séance, épreuve, appel, consultation, réunion, transaction, transport …
Aggrégation/Composition : tout/parties, contenant/contenu, supérieur/subordonné, pays/région, …
Relations entre membres : parenté, collaboration, cercle d'amis, …
…

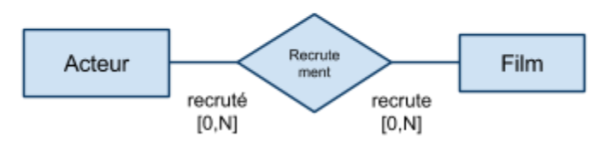
Contraintes de cardinalité

Pour chaque ensemble participant à une association, on précise dans combien d'instances de l'association chaque entité peut apparaître.

On donne en général un intervalle $[b_\text{inf},b_\text{sup}]$ qui définit le nombre d'apparitions autorisées pour chaque rôle de l'association

Représentation graphique

Associations binaires

Associations ternaires

Types d'associations

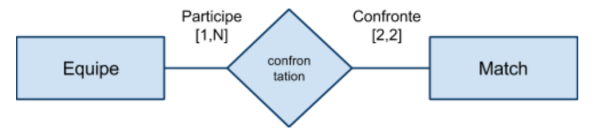
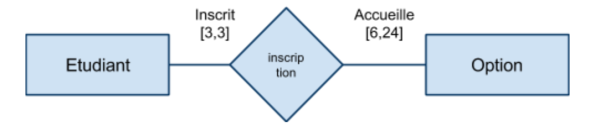
Associations de 1 à plusieurs (fonctionnelle)

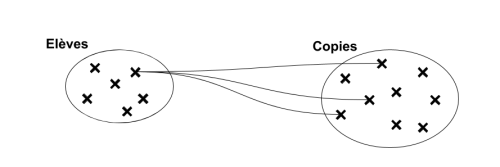
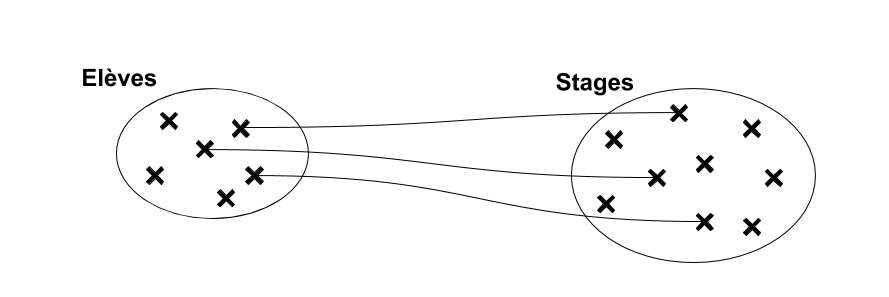
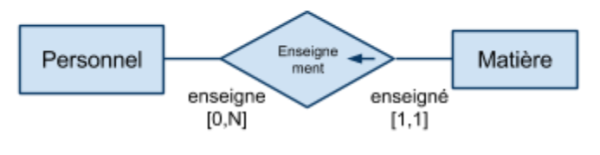
Relation non symétrique entre les deux ensembles : […,1] d'un côté, […,N] de l'autre. Relation de type contenant/contenu, propriétaire/objet possédé, occupant/occupé, actif/passif etc… Il s'agit du type d'association le plus "courant".

On dit parfois que l’ensemble dont la participation est unique est dit “à gauche” de l’association fonctionnelle, et celui dont la participation est multiple est “à droite”, autrement dit la pointe de la flèche désigne l’ensemble de “droite”:

“à gauche” → “à droite”

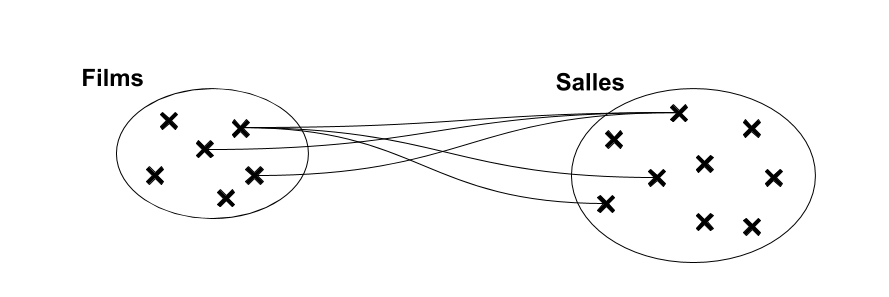
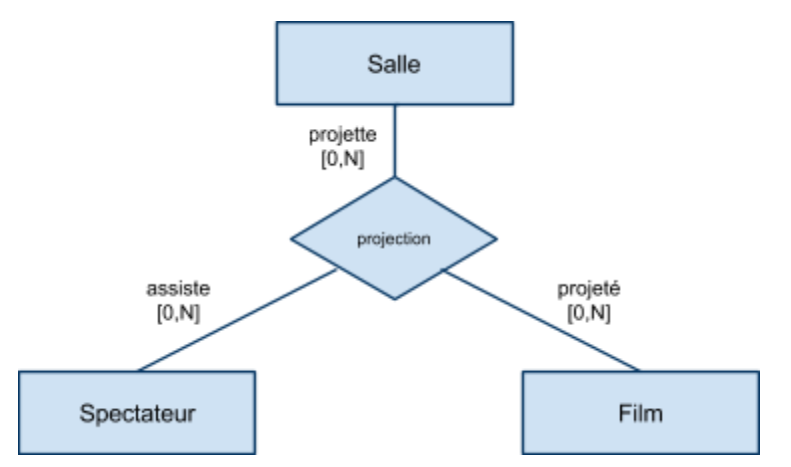
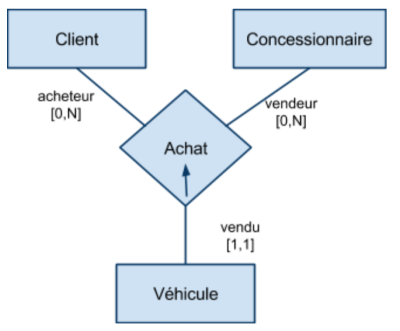
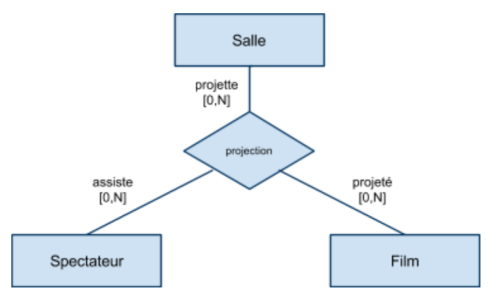
Associations de plusieurs à plusieurs (croisée)

Dans une association “croisée”, les tous les lien de l’association sont de cardinalité multiple […,N]

Modèles Entité Associations valués

Dans le cadre du modèle entité/association :

les attributs des ensembles d'entités sont des mesures:
- Soit $A$ un attribut de l'ensemble d'entités $\mathcal{E}$

$A : \mathcal{E} \rightarrow \text{dom}(A)$

les attributs des associations sont des opérateurs :
- Soit $B$ un attribut de l'association sur $\mathcal{E} \times \mathcal{F}$

$B : \mathcal{E}\times \mathcal{F}\rightarrow \text{dom}(B)$

Mesures

Les mesures sont les données saisies sur les éléments d'un ensemble. Chaque mesure est associée à un attribut.
Le schéma de l'ensemble est l'ensemble des attributs servant à caractériser ses éléments
Les éléments de l'ensemble sont discernables ssi il existe un jeu de mesures différent pour chaque élément de l'ensemble
Une clé est un ensemble d'attributs minimal (permettant de distinguer les objets) appartenant au schéma

TODO

Ensembles discernables / non discernables

Opérateurs

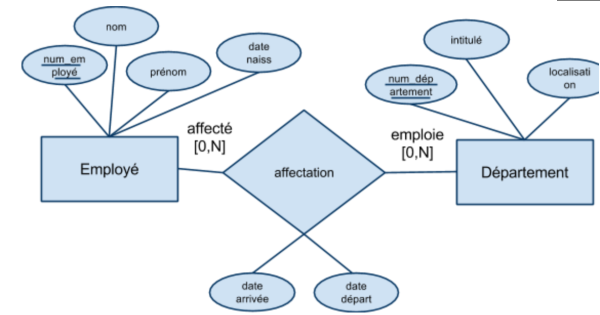
On s’intéresse ici aux associations qui représentent une “opération” (inscription, achat, embauche, affectation…).
Lors d’une mise à jour de la base, certains événements tels que l’emprunt ou le retour d’un ouvrage, l’affectation d’un employé à un poste, ou la liste des anciens clients disparaissent.
Il est possible de garder une trace des événements passés en mettant un (ou plusieurs) attributs sur une association.
Ainsi, certaines associations peuvent être "datées", c'est à dire
- avoir lieu à une date
- ou prendre place sur une durée précise (prêt,accès temporaire, statut temporaire…)
On peut ainsi mémoriser :
- "Monsieur Dupont a été employé au département logistique de tant à tant."…
- "L'étudiant X a été élève Centrale Méditerranée de telle année à telle année"…

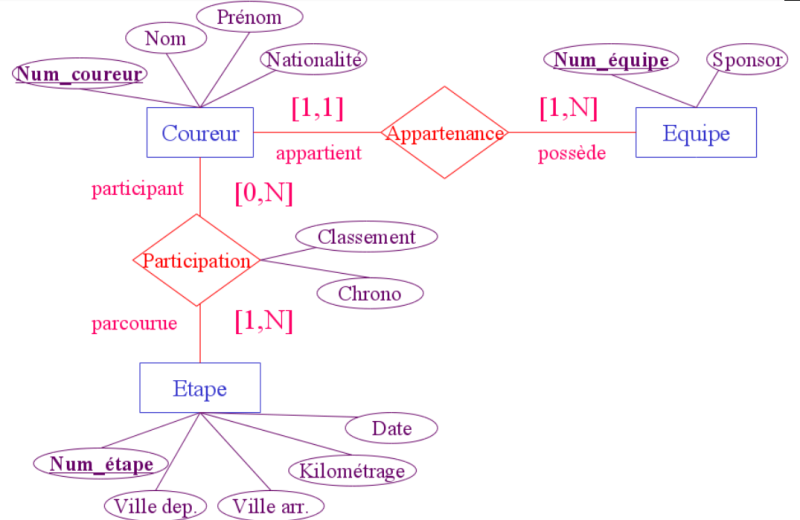
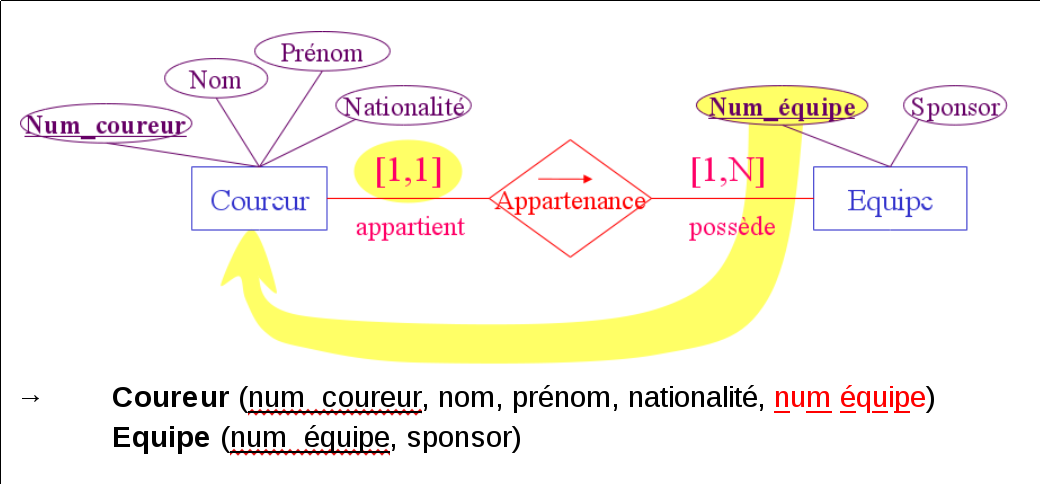
Exemple "Monsieur Dupont a été employé au département logistique de tant à tant."…

Exemple

Chaque coureur est décrit par ses nom, prénom, nationalité et numéro de maillot.
Chaque coureur appartient à une équipe qui possède un numéro, un sponsor associé.
Chaque coureur participe à une ou plusieurs étapes. Une étape se caractérise par son numéro, son type (contre la montre/étape simple), ses points de départ et d'arrivée, sa date.
A chaque étape est associée un classement d'arrivée pour chaque coureur, avec la durée totale de course.

7. Traduction vers le modèle relationnel

Il est possible de traduire un modèle entité/association vers un modèle relationnel (en perdant quelques propriétés).

Lors de la réalisation d'une base de données, on passe en général par les étapes suivantes:

Conception de la base sous forme d'un modèle entité/association.
Traduction sous la forme d'un modèle relationnel.
Normalisation (voir Normalisation d'un schéma)
Mise en œuvre informatique.

Un petit nombre de règles permettent de traduire un modèle entité/association vers un modèle relationnel.

Selon ces règles, à la fois les ensembles d'entités et les associations sont transformés en schémas relationnels.
Les liaisons et dépendances entre schémas de relation sont assurés par la définition des clés étrangères (attributs communs à plusieurs tables).

Schéma de base et clé étrangère

Un schéma (ou modèle) de bases de données est un ensemble fini de schémas de relation.
Une base de données est un ensemble fini de relations.
Les liens et associations entre relations entre s’expriment sous la forme de clés étrangères

Définition

Au sein d'un schéma relationnel $R$ , Une clé étrangère est un attribut (ou un groupe d'attributs) qui constitue la clé primaire d'un schéma $S$ distinct de $R$ .
La présence d'une clé étrangère au sein d'une relation $r$ de schéma $R$ introduit une contrainte d'intégrité sur les données :
- la valeur des attributs de la clé étrangère d'un tuple de $r$ doit être trouvée dans la table s correspondante.
On indique la présence d'une clé étrangère à l'aide de pointillés : {…, Clé étrangère, …}

Exemple

Schéma de base relationnelle :

Clients ( nom_client, adresse_client, solde)
Commandes ( num_Commande, nom client, composant, quantité)
Fournisseurs ( nom_fournisseur, adresse_fournisseur)
Catalogue ( nom_fournisseur, composant, prix )

Traduction des associations de plusieurs à plusieurs

Une association croisée ne contient que des contraintes de cardinalité de type [..,N]. Soit $R$ une telle association et $E_1$ , …, $E_k$ les ensembles participant à l'association.

Règle de traduction :

Chaque ensemble $E_i$ est traduit par un schéma relationnel (contenant les mêmes attributs)
L'association $R$ est traduite sous la forme d'un schéma relationnel contenant:
- les clés primaires des ensembles participant à l’association
- (éventuellement) les attributs propres à l'association,

Traduction :

Pays (nom_pays, superficie, population, PIB )
Matière_première ( nom_matière, unité, prix )
Exportation (nom pays, nom matière, quantité)

Traduction :

Appareil (code_appareil, type, marque, modèle)
Séance (date, heure, local)
Réservation (code appareil,date, heure, local)

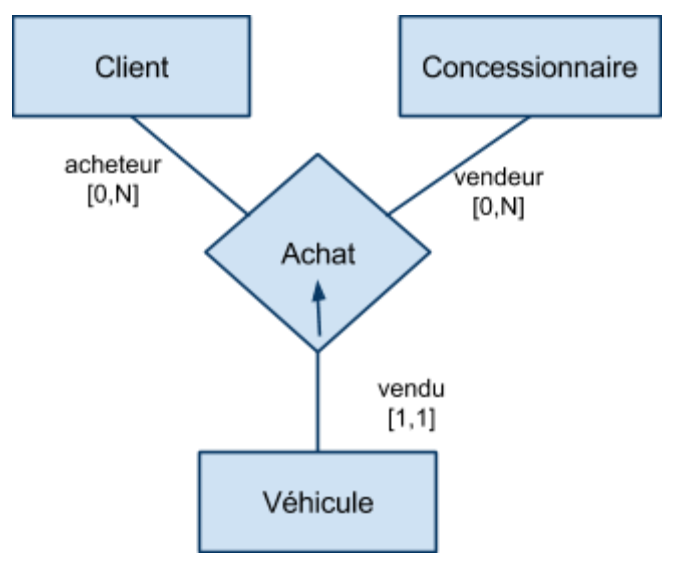
Traduction des associations de un à plusieurs

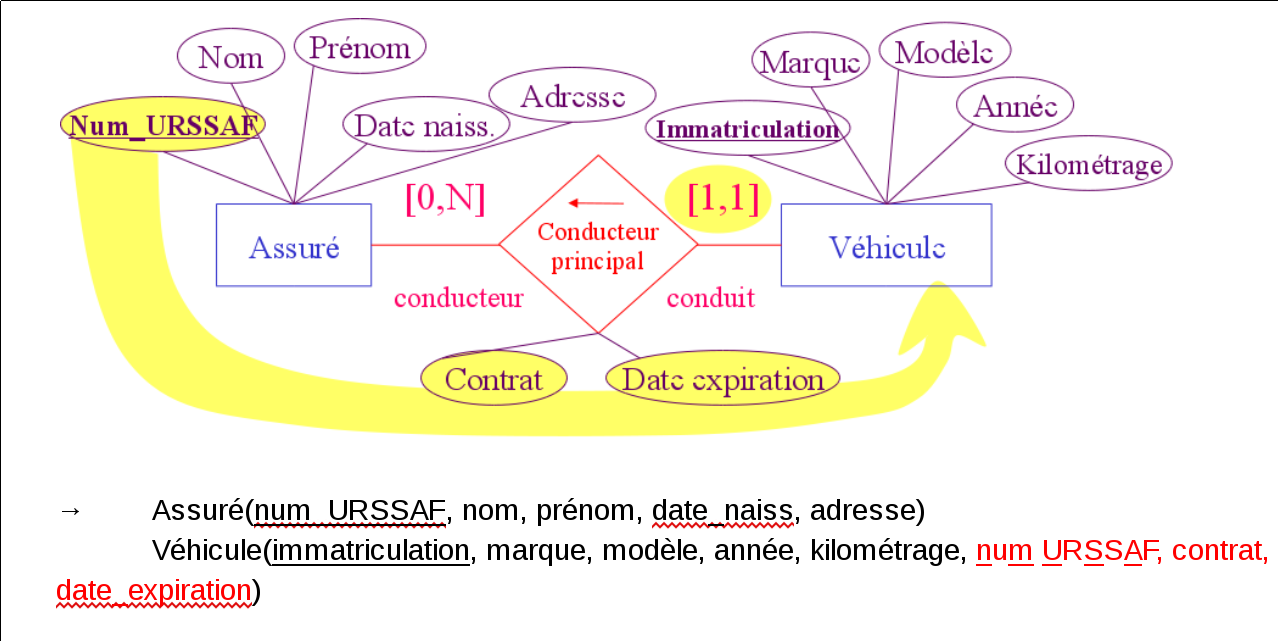
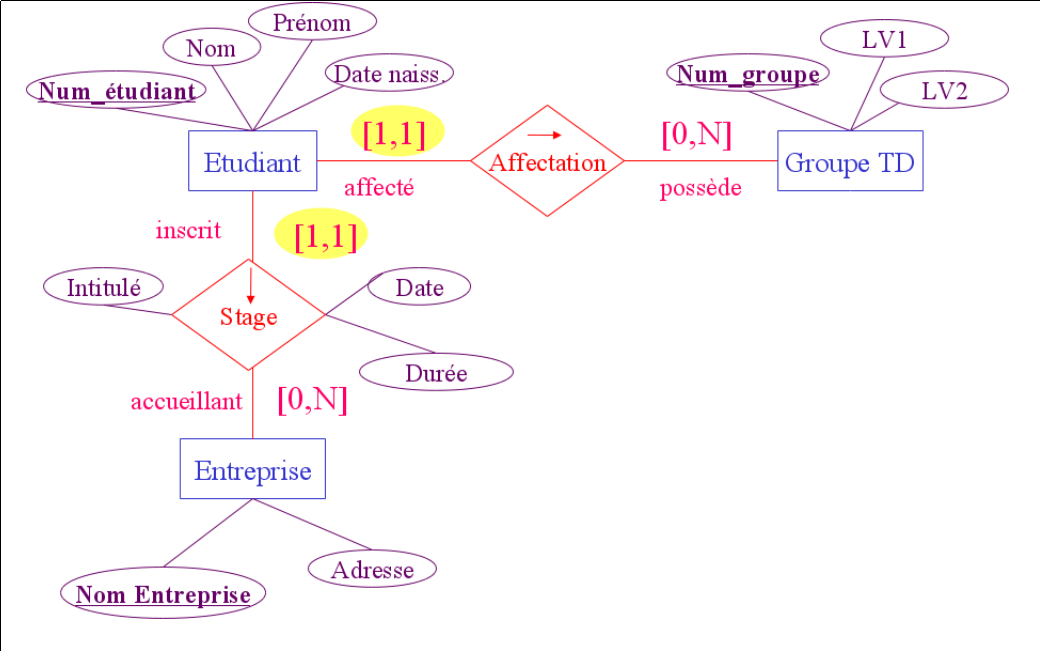
Soit une association fonctionnelle $R$ . On suppose qu'il existe au moins un ensemble $A$ de cardinalité unique [1,1] participant l’association.

Règle de traduction

Chaque ensemble participant est traduit sous forme de schéma relationnel
L'association $R$ est traduite sous forme de clé étrangère : l'ensemble $A$ reçoit la clé primaire du (ou des) ensemble(s) dont la participation est multiple.

Exemple :

Remarque : lorsque l’association est valuée, les attributs de l’association sont également injectés dans la table représentant l’ensemble de gauche.

Exemple

Traduction :

Groupe_TD( num_groupe, LV1, LV2)
Entreprise ( nom_entreprise, Adresse)
Etudiant ( num_etudiant, Nom, Prénom, Date_naiss, num groupe, intitulé, date, durée, nom entreprise)

Exemple complet

Schéma de base relationnelle :

Clients ( nom_client, adresse_client, solde)
Commandes ( num_Commande, nom client, composant, quantité, montant)
Fournisseurs ( nom_fournisseur, adresse_fournisseur)
Catalogue ( nom_fournisseur, composant, prix )

Réalisation :

Clients :

nom_client	adresse_client	solde
Durand	7, rue des Lilas	335,00
Dubois	44, av. du Maréchal Louis	744,00
Duval	5, place du marché	33,00

Commandes :

num_Commande	nom client	composant	quantité
6674	Dubois	micro controller	55
6637	Dubois	radio tuner	2
6524	Durand	transistor	4
6443	Duval	micro controller	7

Fournisseurs :

nom_fournisseur	adresse_fournisseur
Sage	33, College street, London
MoxCom	77 Ashley square,Mumbay

Catalogue :

nom_fournisseur	composant	prix
Sage	transistor	4,4
MoxCom	micro controller	3,7
MoxCom	radio tuner	7,0