Table des matières
CM5 : Indexation / Modèle relationnel
5. L'indexation
Une donnée informatique est un élément d'information ayant subi un encodage numérique
- Consultable/manipulable/échangeable par des programmes informatiques
- Possibilité de la conserver sur un support de stockage numérique (CD-ROM, disque dur, SSD, …)
- Les informations peuvent être stockés dans un fichier (ex : fichier csv).
- Un jeu de valeurs encodé et enregistré est appelé un enregistrement
5.1 Généralités
Pour une gestion efficace des données, il est nécessaire de pouvoir identifier chaque enregistrement de façon unique.
L'indexation des données repose sur un principe simple d'étiquetage consistant à attribuer une étiquette différente à chaque enregistrement. Cette étiquette peut être une suite de caractères arbitraires, un entier, ou un descripteur explicite. On parle en général de clé ou d'identifiant pour désigner cette étiquette.
- L'indexation des données consiste à attribuer à chaque donnée distincte un identifiant unique.
- On parle également de clé de l'enregistrement:
On peut représenter l'opération d'indexation sous la forme d'une fonction. Si $d$ est le jeu de valeurs, $k(d)$ désigne l'identifiant de ce jeu de valeurs.
Unicité
- soient $d_1$ et $d_2$ deux enregistrements,
- si $k(d_1) = k(d_2)$, alors $d_1=d_2$.
Efficacité
L'existence d'un identifiant unique pour chaque jeu de valeurs $d$ permet la mise en œuvre d'une recherche par identifiant (ou recherche par clé).
La recherche par identifiant repose sur une fonction d'adressage $I$ qui à tout identifiant $k$ associe sa position (entrée) $i$ dans un tableau de données: $I : k \rightarrow i$. Ainsi si $k$ est l'identifiant servant à la recherche, l'extraction des informations se fait en 2 étapes:
- $i = I(k)$ (lecture de l'index des données)
- $d = D[i]$ (lecture des données elles mêmes)
Compacité
L'identifiant doit en pratique tenir sur un nombre d'octets le plus petit possible pour que la liste $L$ puisse être manipulée en mémoire centrale. Autrement dit, il faut que :
- $|k| << |d|$
pour que :
- $|L| << |D|$
Utilisation
Définir un ordre sur les données
La présence d'un identifiant permet de définir un ordre total sur les données :
- ordre sur les entiers (identifiant entier)
- ordre alphabétique (identifiant texte)
- ordre ASCIIbétique (chaîne de caractères quelconque)
Lier les données
Dans le cas des bases de données, l'identifiant constitue une référence vers les jeux de valeurs des tableaux de données. Une référence permet de lier les données d'une table aux données d'une autre table.
Exemple :
- Pour chaque album de la table des albums, l'identifiant d'artiste (ici un numéro) permet de lier l'album avec l'artiste (ou groupe) correspondant.
- Pour chaque piste de la table des pistes, l'identifiant d'album permet de lier la piste à l'album correspondant (et donc à l'artiste correspondant par transitivité)
Structure d'ensemble
L'index définit l'appartenance d'une donnée à un ensemble.
Soit $\mathcal{E}$ un ensemble de données indexées : $$ \mathcal{E} = \{d_1, d_2, ..., d_K\} $$ On a l'équivalence : $$ d \in \mathcal{E} \Leftrightarrow k(d) \in I $$
Ainsi, il ne peut y avoir de doublon car $\forall d$ :
- $k(d)$ est unique
- $i = I(k(d))$ est unique ssi $d \in \mathcal{E}$ et indéfini sinon.
5.2 Exemples d'indexation des données
5.2.1 Adressage des tableaux
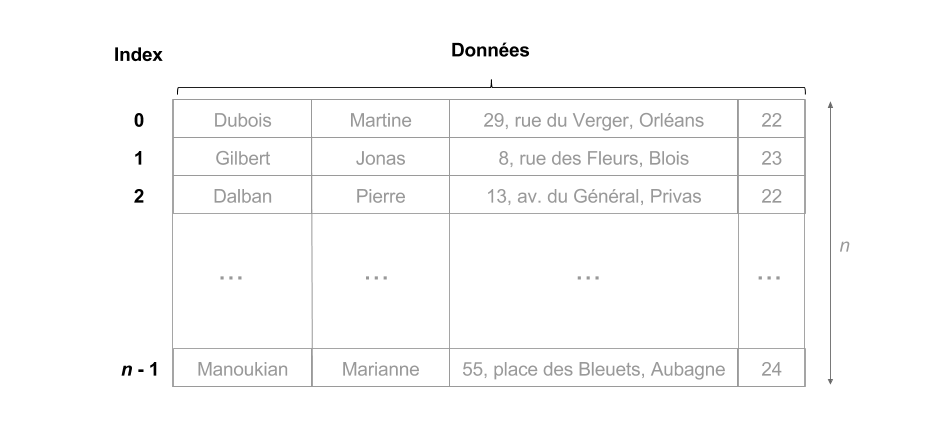
L'exemple le plus simple d'indexation est celui fourni par les numéros de case d'un tableau.
- Soit $D$ un tableau de $n$ lignes
- le numéro $i < n$ est à la fois l'identifiant et l'entrée (ou adresse) de la ligne $D[i]$
5.2.2 Maintenance centralisée d'un index
Dans le cas général, l'identifiant n'est pas égal à l'entrée!
On sépare donc l'index $k$ de l'entrée $i$:
- $k$ est l'identifiant (ou clé) de la donnée $d$. Il s'agit d'une valeur numérique quelconque.
- $i$ est l'entrée de la donnée $d$, correspondant à sa position dans le tableau de données.
- l'intégrité de l'index
- l'unicité de l'identifiant
Il existe différentes méthodes permettant d'assurer l'intégrité de l'index:
- Le programme maintient une liste triée des identifiants déjà utilisées. Lors de l'ajout d'une nouvelle donnée, il s'assure que l'identifiant n'est pas déjà présente dans la liste.
- Coût :
- $O(n)$ en mémoire
- $O(\log n)$ pour l'ajout
- Dans le cas où les identifiants sont des numéros (entiers), il est possible d'utiliser un compteur qui s'incrémente à chaque nouvelle insertion.
- Coût :
- $O(1)$ en mémoire
- $O(1)$ pour l'ajout
- numéro INE (étudiants)
- numéro URSSAF (sécurité sociale)
- numéro d'immatriculation (véhicules)
- numéro de compte en banque
- code barre
- etc.
5.2.3 Indexation pseudo-aléatoire : les fonctions de hachage
Utilisation d'une fonction de hachage :
- qui "calcule" la valeur de l'identifiant à partir des valeurs du jeu de valeurs à insérer.
- La fonction de hachage doit être telle que la probabilité de choisir le même identifiant pour deux données différentes soit extrêmement faible.
Attribution d'un identifiant arbitraire entre 0 et n-1
- Etape 1 : transcodage binaire des données
i = int.from_bytes(d, byteorder='big')- avantage : les données différentes ont un code entier différent
- mais : |i| = |d|
s = 'paul.poitevin@centrale-marseille.fr' d = bytes(s, 'ascii') i = int.from_bytes(d, byteorder='big') print("i =", i)
donne :
i = 852806586114976881510056778471769180697471859150728801241505293627173168229624211058
- Etape 2 : réduction du code
- Méthode 1 : le modulo n (reste de la division entière par n)
k = H(i) = i mod n- Avantage :
- $|k| << |d|$
- Inconvénient:
- deux données différentes peuvent avoir le même code
- ce codage revient à sélectionner les bits de poids faible
- deux données proches ou très similaires auront un index proche ou similaire : si
j = i + 1,H(j) = H(i) + 1(presque toujours) - —> il faut prendre n premier
-
-
- $n = 2^{32} = 4294967296$ :
- H_code(
paul.poitevin@centrale-marseille.fr) =1697539698 - H_code(
martin.mollo@centrale-marseille.fr) =1697539698
- $n = 67280421310721$ (premier):
- H_code(
paul.poitevin@centrale-marseille.fr) =36148249469507 - H_code(
martin.mollo@centrale-marseille.fr) =65330032132071
-
-
- Méthode 2 : combiner produit et modulo – soient m et n deux nombres premiers entre eux
k = H(i) = (i * m) mod n- Avantage :
- $|k| << |d|$
- deux entiers proches donneront auront des codes très différents : si
j = i + 1,j * m - i * m = m
- Inconvénient :
- deux données différentes peuvent avoir le même code
- le produit
i * mpeut etre coûteux à calculer
- Méthode 3 : Hachage cryptographique :
- Le hachage cryptographique est construit de telle sorte qu'il soit très difficile de trouver un entier
j != itel queH(i) = H(j). - Un tel code est appelé une "signature".
- Exemples :
Exemple
Le gestionnaire de bases de données MongoDB utilise une indexation des données par clé cryptographique.
5.3 Généralisation : multi-indexation
5.4 Structures de données pour l'indexation
5.4.1 Liste triée
5.4.2 Index bitmap
5.4.3 Les B-arbres
Que faire lorsque l'index ne tient pas en totalité dans la mémoire centrale ?
- L'index est découpé en "blocs"
- Les blocs sont organisés sous la forme d'un arbre (B-arbre = "Balanced Tree")
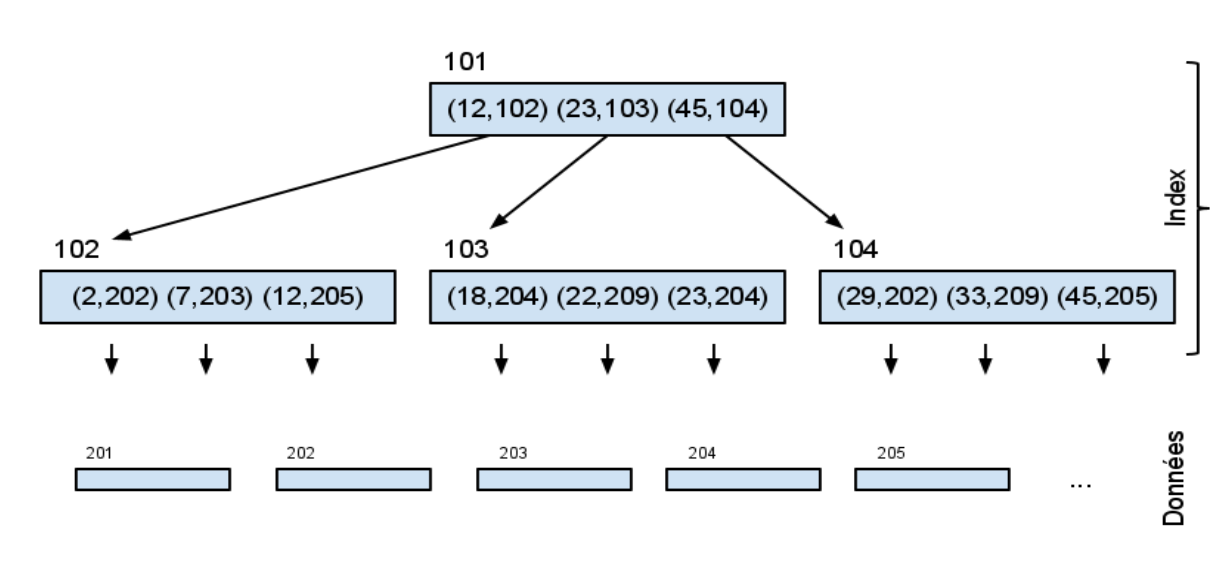
Considérons un index composé de couples (clé, numero de page). On suppose que l’index est également découpé en pages, chaque page d'index contenant au maximum b clés. Si l’index comporte beaucoup de pages, il est intéressant de l’organiser hiérarchiquement en pages et sous-pages, selon une organisation appelée "B-arbre" (Balanced Tree):
- chaque noeud de l’arbre contient une liste croissante de couples (clé, numéro d’une sous-page)
- chaque clé est dupliquée dans sa sous-page :
- les clés contenues dans la sous-page sont inférieures ou égales à elle,
- les clés contenues dans la sous-page sont strictement supérieures à celles de la sous-page précédente.
- les feuilles contiennent des couples (clé, numéro de la page du tableau de données)
- paramètre d’entrée : k
I ← charger la racine de l’arbre
tant que I n’est pas une feuille :
k’ ← première clé de I
tant que k > k’
k’ ← clé suivante
I ← charger sous-page de k’
Remarque : Pour que l’accès aux données soit efficace,
- il faut que l’arbre soit le moins profond possible : arbre “équilibré”.
- Dans ce cas,
- chaque noeud a
bfils, - et la profondeur de l’arbre est de l’ordre de logb(N).
- Pour charger la page contenant le tuple cherché,
- il faut donc logb(N) + 1 lectures sur disque.
En pratique, il existe des algos permettant d’assurer que chaque noeud contient entre b/2 et b clés (sauf la racine).
6. Le modèle relationnel
On introduit dans ce chapitre le modèle relationnel qui sert de fondation à la conception de bases de données.
Les différents modèles utiles en représentation des connaissances reposent sur des notions de base de la théorie des ensembles :
- Ensemble finis
- Éléments partiellement (ou totalement) discernables
6.1 Schéma de données
Schémas de données
- Un enregistrement est un jeu de valeurs organisé sous forme de tuple
- A un tuple on associe en général un schéma de données.
- Définir un schéma consiste à définir :
- une liste d'attributs (labels) associées à chacune des valeurs du tuples.
- A chaque attribut correspond :
- un intitulé
- un domaine de valeurs (type/format des données)
Tableau de données
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
- Soit $R(A_1, ..., A_m)$ un schéma.
- On note $\text{dom}(A_i)$ le domaine associé à l'attribut $A_i$.
- On dit d'un tuple $t$ qu'il obéit au schéma $R$ si les valeurs qu'il contient correspondent aux domaines des attributs du schéma.
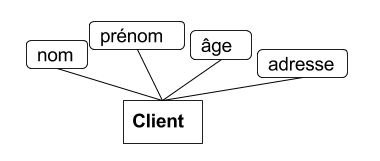
UML :
Client(nom, prénom, adresse, âge)
Étudiant(nom, prénom, adresse, INE)
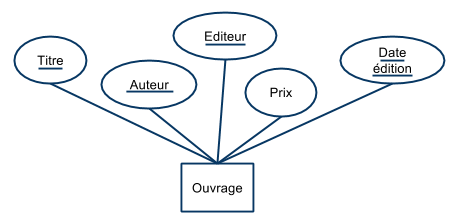
Ouvrage(titre, auteur, éditeur, prix, date_édition)
Véhicule(immatriculation, marque, modèle, couleur)
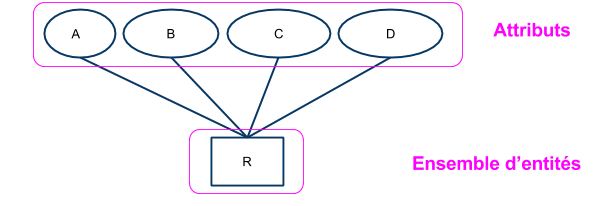
6.1.1 Entité et attributs
- Une entité $x$
- est une représentation d'un objet du monde réel,
- appartenant au système/à l'organisation modélisée.
- Une entité est décrite par une ou plusieurs valeurs caractéristiques, appelées attributs.
- Chaque attribut :
- a un nom unique dans le contexte de cet ensemble d'entités : $A$, $B$, $C$, $A_1$, $A_2$, …, $A_m$, …
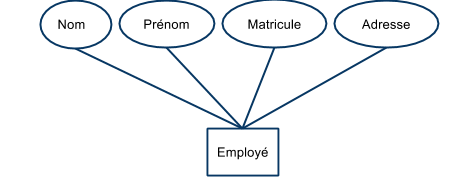
- Exemples de noms concrets : couleur, nom, horaire, salaire.
- prend ses valeurs dans un domaine bien spécifié,
- également appelé le type de l'attribut.
- Le domaine d'un attribut est noté $\text{dom}(Aj)= Dj$.
- Exemples :
- $\text{dom}(couleur)={rouge, vert, bleu, jaune}$,
- $\text{dom}(nom) = $ensemble des chaînes de caractères,
- $\text{dom}(salaire) =$ entiers naturels
- etc…
- Un attribut $A_j$ est une fonction à valeur sur $D_j$ :
$$A_j : E \rightarrow D_j$$ $$x \mapsto A_j(x)$$
- Un attribut peut être :
- simple ou composé.
- Exemple : une adresse peut être décrite par une simple chaîne de caractères, ou peut être décomposée en rue , no, boîte, ville, code postal, pays.
- obligatoire ou facultatif ($D_j$ peut ou non contenir la valeur ø ).
- atomique ou non (Un attribut peut posséder 0, 1 voire plusieurs valeurs…)
6.1.2 Ensembles d’entités et schéma d’ensemble
Un ensemble d'entités est un ensemble fini d'éléments : $$E = \{x_1,…,x_n\}$$ Il regroupe (ou associe) plusieurs entités ayant des caractéristiques communes (descriptibles à l'aide du même ensemble d'attributs).
- les employés d'une firme,
- les cours de Centrale Méditerranée,
- une collection de disques,
- etc…
- Les éléments d’un ensemble d’entités sont partiellement discernables à travers les valeurs de leurs attributs :
- les attributs $(A_1,...,A_m)$ servent à décrire les éléments de l’ensemble.
- Le schéma $R$ de l’ensemble $E$ est une application de l'ensemble d'entités vers l'ensemble des tuples de schéma $R$
- Soit :
$$ R : \mathcal{X} \rightarrow D_1 \times ... \times D_m$$ $$ x_i \mapsto (A_1(x_i),…, A_m(x_i))$$
6.1.3 Relation
La Relation est la représentation logique d'un tableau de données.
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
Soit $R = (A_1,...,A_m)$ un schéma de données
Une relation $r$ obéissant au schéma $R$ est un sous-ensemble du produit cartésien $\text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- avec :
- $\forall (i,j), a_{ij} \in \text{dom}(A_j), $
- $\forall i, t_i \in \text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- $n$ : nombre de tuples
- $m$ : nombre d'attributs par tuple
- Le schéma $R$ représente le niveau abstrait (modélisation)
- La relation $r$ représente un cas concret de réalisaton (à un schéma $R$ peuvent correspondre une infinité de réalisations possibles : $r$, $r'$, $r''$, etc. )
6.2 Dépendances fonctionnelles
- Au sein d'un schéma $R$,
- Il peut exister un ensemble de contraintes, noté $F$,
- portant sur les attributs (plus précisément sur les valeurs prises par les attributs).
- L'ensemble F est indépendant de R.
- On parle de contraintes d’intégrité.
- Ces contraintes s’expriment sous la forme de dépendances fonctionnelles.
- Relation binaire : une relation binaire $r$ portant sur deux domaines $A$ et $B$:
- est un sous-ensemble du produit cartésien $A \times B$.
- si $(a,b) \in r$, on note parfois $a r b$ ce qui signifie “a est en relation avec b”.
- Fonction : une fonction $f : A \rightarrow B$ est une relation binaire sur $A \times B$ telle que
- pour tout $a \in A$,
- il existe un unique $b$ tel que $(a,b) \in f$.
- On note $b=f(a)$ ,
- ce qui signifie qu'au sein de la relation $f$, $b$ est déterminé de façon unique par le choix de $a$ (autrement dit : “b dépend de a”)
- Soit $r$ une relation définie selon $R(A_1,...,A_m)$
- Soient $X$ et $Y$ deux sous-ensembles de $R$
- On dit que la relation $r$ définit une dépendance fonctionnelle de $X$ vers $Y$,
- notée $X \stackrel{r}{\rightarrow} Y$
- si les valeurs de $r$ permettent de définir une fonction de $d(X)$ vers $d(Y)$.
Soit la relation $r$:
| A | B | C |
|---|---|---|
| 1 | a | e |
| 2 | b | f |
| 2 | c | f |
| 3 | d | k |
| 4 | d | k |
- On a les dépendances suivantes :
- $A \rightarrow C$
- $B \rightarrow C$
- mais pas : $A \rightarrow B$, $B \rightarrow A$, ni $C \rightarrow A$
- On a aussi :
- $A,B \rightarrow C$
- mais pas : $B,C \rightarrow A$, ni $A,C \rightarrow B$, etc.
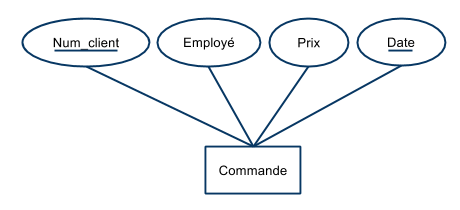
- Soit le schéma :
- Commande (num_client, quantité, prix, date, num_article)
- et l’ensemble de contraintes
$$ \begin{array}{rl}F &= \{\\ & \text{num_client, date} \rightarrow \text{num_article, quantité, prix} \\ & \text{num_article, quantité} \rightarrow \text{prix} \\ &\} \end{array} $$
- La première contrainte indique qu'il ne peut y avoir deux factures émises pour un même client à une date donnée.
- La seconde contrainte indique que le prix payé dépend de l’article et de la quantité commandée.
- Soit le schéma :
- Ouvrage (titre, auteur, éditeur, prix, date_edition)
- et la contrainte :
- {titre, auteur, éditeur → prix, date_édition}
La contrainte signifie :
- “pour une oeuvre chez un certain éditeur, une seule édition est possible (pas de réédition à une date ultérieure)”
- “politique du prix unique”
- Réservation(code_appareil, date, heure, salle)
Exprimer la dépendance fonctionnelle :
- « Un appareil ne peut pas être utilisé dans deux locaux différents au même moment »
- Il importe donc de bien réfléchir, au moment de l'étape de conception,
- du réalisme et du caractère limitant de certaines dépendances fonctionnelles,
- et du caractère éventuellement limitant du choix des attributs.
- Ainsi, le schéma décrivant les commandes (exemple 2)
- ne permet pas de commander des articles de nature différente au sein d'une même commande
- (un client, pour commander deux râteaux et une truelle, doit donc effectuer deux commandes, qui plus est à des dates différentes!).
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Définir des dépendances fonctionnelles sur cet ensemble d'attributs
6.3 Clé d'une relation
6.3.1 Définitions
- Soit un schéma $R(A_1, ..., A_m)$.
- Une clé $K$ :
- est un ensemble minimal d'attributs inclus dans R,
- tel que toute relation $r$ de schéma $R$ définit une dépendance fonctionnelle de $d(K)$ dans $d(R)$,
- cette dépendance est notée $K \rightarrow R$.
- Remarques :
- Si un schéma $R$ possède une clé $K$, alors tous les éléments d’une relation $r$ de schéma $R$ sont discernables : la valeur de la clé permet d’identifier de façon unique chaque élément de l’ensemble.
- Au sein d'un schéma, il est souvent possible de définir plusieurs clés à partir des attributs. Le concepteur du modèle choisit une clé parmi les clés possibles. Cette clé est appelée clé primaire.
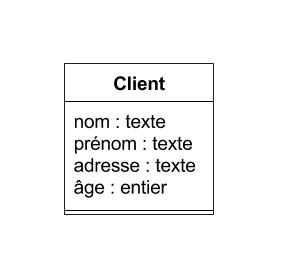
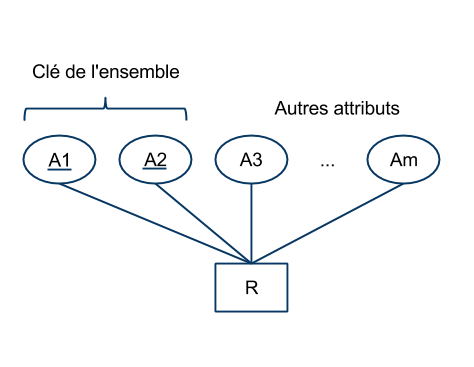
- Graphiquement, les attributs constituant la clé sont soulignés:
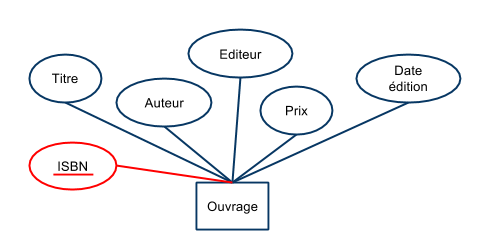
- Pour certains schémas,
- il est courant de définir comme clé un entier identifiant de façon unique chaque élément de l'ensemble (appelé identifiant ou “Id”).
- La clé est alors constituée de cet attribut unique.
Représentation UML :

6.3.2 Axiomes d'Amstrong
Soit $K$ une clé candidate. On démontre que $K \rightarrow R$ à l'aide des axiomes d'Amstrong à partir d'un ensemble de DF connues:
- Réflexivité : $$Y \subseteq X \Rightarrow X \rightarrow Y$$
- Augmentation : $$X \rightarrow Y \Rightarrow X,Z \rightarrow Y,Z$$
- Transitivité : $$X \rightarrow Y \text{ et } Y \rightarrow Z \Rightarrow X \rightarrow Z$$
- Pseudo-transitivité : $$X \rightarrow Y \text{ et } Y,W \rightarrow Z \Rightarrow X,W \rightarrow Z$$
- Union : $$X \rightarrow Y \text{ et } X \rightarrow Z \Rightarrow X \rightarrow Y,Z$$
- Décomposition : $$X \rightarrow Y, Z \Rightarrow X \rightarrow Y \text{ et } X -> Z$$
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Montrer que l'ensemble {num_train, num_voiture, num_place, date, gare_départ} est une clé primaire du schéma?
6.4 Normalisation d'un schéma
Tables mal construites
$$\textbf{Fournisseur}(\underline{\text{nom_f, composant}}, \text{adresse_f, prix})$$
- Problèmes :
- Redondance : l’adresse des fournisseurs est répétée plusieurs fois
- Inconsistance : mauvaise mise à jour ⇒ adresses différentes pour un même fournisseur.
- Problème Insertion : on ne peut pas insérer dans la table un fournisseur qui ne fournit rien
- Problème suppression : si un fournisseur ne fournit plus rien, on perd son adresse
- Solution?
- Couper la table en 2?
–> Impossible de retrouver les prix pratiqués par les différents fournisseurs.
- Nouveau Schéma :
–> Il est possible de reconstruire la table initiale en effectuant une jointure entre ces 2 tables sur l’attribut nom_f.
- Enseignement (id_enseignant, nom_enseignant, matière, id_élève, nom_élève)
- Arrêt (num_train, horaire, nom_gare, ville)
- Facture (id_client, article, date, montant)
6.5 Formes Normales
Les Formes normales
- Restreignent les dépendances admises dans un schéma relationnel
- Permettent d’éviter la duplication de l’information au sein des relations
- Définissent une méthode
- de décomposition d’un schéma relationnel redondant
- en plusieurs schémas liés entre eux:
6.5.1 2ème forme normale (2FN)
- Soit $R$ un schéma relationnel
- Soit $X$ un ensemble d’attributs ⊆ $R$
- Soit $A$ un attribut de $R$
- Il existe une DFE entre $X$ et $A$ ssi :
- $X \rightarrow A$
- Il n’existe aucun sous-ensemble $Y$ ⊆ $X$ tel que $Y \rightarrow A$
- Un schéma $R$ est en 2FN :
- ssi la clé primaire de $R$ est en DFE avec tous les autres attributs.
- Donc : il n’y a pas d’attributs qui ne dépendent que d’une partie de la clé.
6.5.2 Normalisation 2FN
- Lorsqu’un schéma relationnel n’est pas en deuxième forme normale, il doit être normalisé:
- Pour obtenir un schéma 2FN:
- on “découpe” la table selon les DFE trouvées entre les attributs de la clé et ceux qui ne sont pas dans la clé.
- La normalisation consiste:
- à créer une nouvelle table pour chaque DFE ainsi trouvée.
- Soit :
$$\mathbf{R} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,\color{red}{B_j},...,B_m)$$
- avec :
$$\color{red}{A_i} \stackrel{DFE}{\rightarrow} \color{red}{B_j}$$ $$A_1,...,\color{red}{A_i},...,A_n \stackrel{DFE}{\rightarrow} B_1,...,B_{j-1},B_{j+1}...,B_m$$
- Alors le schéma de table doit être modifié comme suit :
$$\mathbf{R_1} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,B_{j-1},B_{j+1}...,B_m)$$ $$\mathbf{R_2} (\underline{\color{red}{A_i}},\color{red}{B_j})$$
Même si aucun attribut ne dépend plus de la clé primaire initiale, il est important de la conserver dans une table spécifique (elle sert à “lier” les valeurs dispersées dans les différentes tables).
- Avant:
$$\textbf{Fournisseur}(\underline{\text{nom_f,composant}}, \text{adresse_f, prix})$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$ $$\text{nom_f, composant} \rightarrow \text{prix}$$
- Après:
$$\textbf{Catalogue}(\underline{\text{nom_f,composant}}, \text{prix})$$ $$\textbf{Fournisseur}(\underline{\text{nom_f}}, \text{adresse_f})$$
- Les tables ont un attribut commun : nom_f (clé primaire de la table Fournisseur).
- La clé primaire de la table des Fournisseurs est dupliquée dans la table des prix (appelée ici Catalogue).
- On dit que nom_f est une clé étrangère de la table des prix (l’attribut fait référence à la clé primaire d’une autre table, en l’occurrence la table des fournisseurs - voir 3.1.1).
6.5.3 3ème forme normale (3FN)
La dépendance fonctionnelle entre 2 attributs $A_i$ et $A_j$ est directe s’il n’existe pas de $A_k$ tel que : $$A_i \rightarrow A_k \rightarrow A_j$$
Un schéma est 3FN :
- S’il est 2FN
- Si tous les attributs sont en DFD avec la clé.
$$\textbf{Commande} (\underline{\text{num_commande}}, \text{nom_f, adresse_f, composant, quantité})$$ $$\text{num_commande} \rightarrow \text{nom_f, composant, quantité}$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$
Le schéma n’est pas 3FN!! (dépendance transitive entre num_commande et adresse)
6.5.4 Normalisation 3FN
* Lorsqu’un schéma relationnel n’est pas en troisième forme normale, il doit être normalisé:
- On crée une table pour chaque DFD trouvée au sein des attributs n'appartenant pas à la clé.
Soit : $$R (\underline{A_1,...,A_m},B_1, ..., \color{red}{B_i},...,\color{red}{B_j},...,B_n)$$ avec : $$A_1, ..., A_m \stackrel{DFD}{\rightarrow} B_1, ...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n$$ $$\color{red}{B_i} \stackrel{DFD}{\rightarrow} \color{red}{B_j}$$ Alors : $$R_1 (\underline{A_1,...,A_m},B_1,...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n)$$ $$R_2 (\underline{\color{red}{B_i}},\color{red}{B_j})$$
Comme précédemment, il est important de conserver la clé primaire de la table initiale si elle permet d'associer les valeurs dispersées dans les tables.
Avant :
- Commande (num_commande, nom_f, adresse_f, composant, quantité)
- avec :
- num_commande → nom_f, composant, quantité
- nom_f → adresse_f
Après :
- Commande (num_commande, nom_f, composant, quantité)
- Client (nom_f, adresse_f)
L’attribut nom_f est maintenant clé primaire de la table Client et clé étrangère de la table Commande.