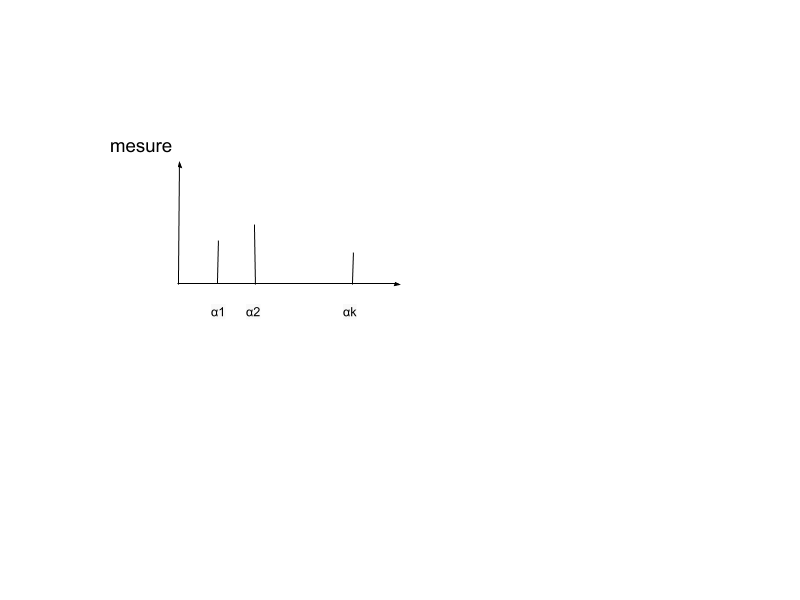Table des matières
3. Statistiques sur les textes
Soit un document $d$ :
- constitué de $T$ symboles $d[1]$, …, $d[i]$, ….
- appartenant à l'alphabet $A = \{\alpha_1,...,\alpha_K\}$ constitué de $K$ symboles.
Une description statistique d’un texte correspond à un histogramme qui porte sur un ensemble de symboles :
Grâce à ces mesures, on souhaite pouvoir comparer 2 textes : $d_1$ et $d_2$. On veut trouver les distances / similarités basée sur cette mesure
- l’ordre des symboles ou des termes est ignoré
- le sens du texte est ignorée
on utilise la théorie de l’information
- information
- divergence KL
- Entropie, entropie croisée
- chaque $d_i$ est la réalisation d'un tirage aléatoire
- obéissant à une distribution de probabilité $p$
- des caractères appartenant à un alphabet
- des termes appartenant à un vocabulaire
3.1 Modèles probabilistes
Les modèles probabilistes interprètent les données de type texte comme étant générées par une distribution de probabilité $P$ inconnue.
La distribution $P$ définit le langage utilisé dans le texte. On ne s'intéresse pas au sens du message, on regarde seulement comment les symboles se répartissent dans les documents, leurs fréquences d'apparition, les régularités, …
Fréquence d'un symbole
Soit $\alpha \in A$ un symbole de l'alphabet. On note $P(X=\alpha)$ la fréquence d'apparition de ce symbole dans le langage $\mathcal{L}$ considéré, soit~: $$P(X=\alpha) = \frac{|\omega \in \Omega : X=\alpha|}{|\Omega|}$$ où $\Omega$ représente l'ensemble des productions de caractères.
On a par définition~: $$\sum_{\alpha \in V} P(X=\alpha) = 1$$
La fréquence empirique du symbole $\alpha$ dans le document $d$ est donnée par~:
où |d| est le nombre de caractères dans le document.

- Voir aussi : Analyse Fréquentielle sur Wikipedia
Représentation vectorielle
On suppose que les caractères d'un langage $\mathcal{L}$ donné sont numérotés de 1 à $K$, soit $A_\mathcal{L} = \{\alpha_1,...,\alpha_k,...\alpha_K\}$.
On notera $\boldsymbol{p}_\mathcal{L}$ le vecteur des fréquences des caractères dans un langage $\mathcal{L}$ donné, où $p_\mathcal{L}(k)$ donne la fréquence du $k^{ème}$ caractère.
- $p_1 = 0.0942$ est la fréquence de la lettre 'A',
- $p_2 = 0.0102$ est la fréquence d'apparition de la lettre 'B'
- etc.
avec bien sûr : $$\sum_{k\in\{1,...,K\}} p_\mathcal{L}(k) = 1$$
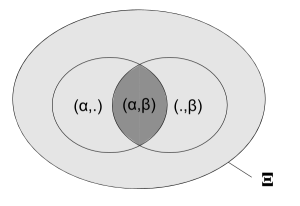
Probabilité jointe
On s'intéresse maintenant aux fréquence d'apparition de couples de lettre successives.
Soient $\alpha$ et $\beta$ deux symboles de l'alphabet.
La probabilité jointe est définie comme : $$P(X=\alpha, Y=\beta) = \frac{|\xi \in \Xi : (X,Y)=(\alpha,\beta)|}{|\Xi|}$$ où $\Xi$ est l'ensemble des productions de couples de caractères.
avec par définition: $$\sum_{(\alpha,\beta) \in A\times A} P(X=\alpha,Y=\beta) = 1$$
La probabilité jointe empirique est donnée par~:
- Les séquences de deux caractères sont classiquement appelées des bigrammes.
- On définit de même les trigrammes comme les séquences de trois caractères
- etc.
Représentation matricielle
On notera $\boldsymbol{P}_\mathcal{L}$ la matrice des fréquences des bigrammes dans un langage $\mathcal{L}$ donné, où $P_{ij}$ donne la fréquence du bigramme $(\alpha_i,\alpha_j)$.
où
- $P_{11} = 1.5 \times 10^{-5}$ est la fréquence du bigramme 'AA',
- $P_{12} = 116.8 \times 10^{-5}$ est la fréquence d'apparition du bigramme 'AB'
- etc.
avec bien sûr : $$\sum_{(i,j) \in \{1,...,K\}^2} P_{ij}=1$$
Corpus de documents
Soit $B$ un corpus de documents, constitué de $n$ documents.
La fréquence jointe du couple $(\alpha,\beta)$ est donnée par $$f_B(\alpha,\beta) = \frac{|\{(i,j):d_i \in B,(d_i[j],d_i[j+1]) = (\alpha,\beta) \}|}{|B|-n} $$
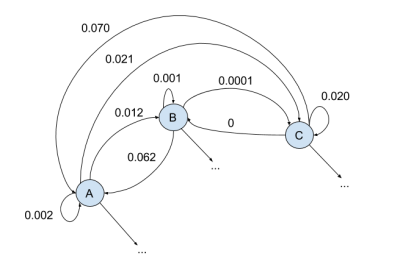
Probabilité conditionnelle
La probabilité conditionnelle du caractère $\beta$ étant donné le caractère précédent $\alpha$ est définie comme :
$$P(Y = \beta | X=\alpha) = \frac{|\xi \in \Xi : (X,Y)=(\alpha,\beta)|}{|\xi \in \Xi : X = \alpha|}$$
qui se calcule empiriquement comme :
$$f_d(\beta|\alpha) = \frac{|\{i:d[i] = \alpha,d[i+1] = \beta\}|}{|\{j:d[j] = \alpha\}|}$$
- La probabilité $P(.|\alpha_i)$ se représente sous forme vectorielle~: $$\boldsymbol{\mu}_i = (P(\alpha_1|\alpha_i), P(\alpha_2|\alpha_i), ...) $$ où $\alpha_1$ est le premier caractère de l'alphabet, $\alpha_2$ le deuxième etc, avec $$\sum_j \boldsymbol{\mu}_{ij} = 1$$
- L'ensemble des probabilités conditionnelles $P(.|.)$ peut se représenter sous une forme matricielle~:
$$ \begin{array}{cl} M &= \left( \begin{array}{c} \boldsymbol{\mu}_1\\ \boldsymbol{\mu}_2\\ ... \end{array} \right) \\ &=\left( \begin{array}{cccc} P(\alpha_1|\alpha_1)& P(\alpha_2|\alpha_1)& P(\alpha_3|\alpha_1)&...\\ P(\alpha_1|\alpha_2)& P(\alpha_2|\alpha_2)& P(\alpha_3|\alpha_2)&...\\ &...&&& \end{array} \right) \end{array} $$
Sachant que $P(\alpha) = \sum_{\beta \in A} P(\alpha, \beta)$, on a : $$\boldsymbol{\mu}_i = \frac{P_{i,:}} {p_i}$$
Soit en français :
- $M_{11}$ est la probabilité de voir un 'A' suivre un 'A'
- $M_{12}$ est la probabilité de voir un 'B' suivre un 'A'
- etc.
- La production d'un mot ou d'un texte est modélisée comme un parcours aléatoire sur une chaîne de Markov définie par la matrice de transitions $M$.
- La fréquence d'apparition des lettres est modélisée comme la mesure stationnaire de la chaîne de Markov, autrement dit le vecteur de probabilité vérifiant : $$ \boldsymbol{p} = \boldsymbol{p} M$$
3.2 Comparer des documents
On considère deux langues $\mathcal{L}_1$ et $\mathcal{L}_2$ utilisant le même alphabet. La différence de fréquence des caractères dans ces deux langages permet de les distinguer. il est ainsi possible de définir une distance entre deux langages basée sur les histogrammes de fréquence empirique des caractères dans les deux langages.
L’information apportée par la lecture du symbole $\alpha$ est définie comme : $$I(\alpha) = -\log_2(P(X = \alpha)) $$ où $p_\alpha = P(X = \alpha)$ est la fréquence d’apparition de ce symbole dans la langue considérée.
L'information est une mesure de la "surprise" provoquée par l'apparition du symbole $\alpha$. Si le symbole $\alpha$ est “rare” ($p_\alpha$ petit), l’information qu’il apporte est élevée. Si le symbole est fréquent, l’information qu’il apporte est faible.
Entropie
L’entropie d’une langue est définie comme l'espérance de l'information apportée par un caractère. $$H(\mathcal{L}) = E_X(I(X)) = -E_X(\log_2(P(X)) $$ i.e. $$H(\mathcal{L}) = - \sum_{k \in \{1,...,K\}} P(X = \alpha_k) \log_2(P(X = \alpha_k))$$
- pour quels types de distribution l’entropie est-elle minimale? maximale?
- quelle est l’entropie d’un message dont les probas d’apparition des termes obéissent à une loi de puissance :
$$C = \frac{1} {\sum_k \frac{1}{k}}$$ $$p(\alpha_k) = \frac{C}{k}$$
Divergence de Kullback-Leibler
Pour comparer deux langues $\mathcal{L}_1 et \mathcal{L}_2$, on peut utiliser la divergence de Kullback-Leibler définie comme l'espérance de la différence des informations apportées par un même symbole:
$$D(\mathcal{L}_1||\mathcal{L}_2) = \sum_{k \in \{1,...,K\}} P_1(X = \alpha_k) \log_2 \left(\frac{P_1(X = \alpha_k)}{P_2(X = \alpha_k)}\right)$$
où $P_1$ désigne la distribution des symboles du langage $\mathcal{L}_1$ et $P_2$ la distribution des symboles du langage $\mathcal{L}_2$.
- La divergence de K-L est positive.
- Elle vaut 0 si les deux distributions sont identiques.
Comparer 2 messages
Soient $d_1$ et $d_2$ deux textes pour lesquels on a calculé les histogramme des fréquences empiriques: $f_1$ et $f_2$ .
La divergence empirique de Kullback Leibler est une mesure de dissimilarité (l'inverse d'une similarité) qui estime combien $d_1$ diffère de $d_2$ $$D(d_1||d_2) = \sum_{\alpha \in d_1 \bigcap d_2} f_1(\alpha) \log_2 \left(\frac{f_1(\alpha)}{f_2(\alpha)}\right)$$
Classer des messages
Il arrive que l'on ne sache pas à l'avance si une suite de symboles $m[1], ... m[T]$ est générée par le langage $\mathcal{L}_1$ (dont les symboles obéissent à la distribution $p_1$) ou le langage $\mathcal{L}_2$ (dont les symboles obéissent à la distribution $p_2$).
Soit $f$ la fréquence empirique des symboles de $m$.
Si $m$ est produit par $\mathcal{L}_1$, on devrait avoir : $$D(f||p_1) < D(f||p_2)$$ soit $$ \sum_{\alpha \in d} f(\alpha) \log_2 \left(\frac{f(\alpha)}{p_1(\alpha)}\right) < \sum_{\alpha \in d} f(\alpha) \log_2 \left(\frac{f(\alpha)}{p_2(\alpha)}\right)$$ soit : $$ \sum_{\alpha \in d} f(\alpha) \log_2 \left(\frac{p_1(\alpha)}{p_2(\alpha)}\right) > 0$$
- Si Test > 0, il est plus probable que $m$ obéisse au langage $\mathcal{L}_1$
- Si Test < 0, il est plus probable que $m$ obéisse au langage $\mathcal{L}_2$
On peut ainsi produire un classifieur basé sur les modèles probabilistes $p_1$ et $p_2$.
Utilisation :
- Deviner la langue d'un document
- Distinguer les messages frauduleux des messages courants
- etc.