TD 1 : Indexation des données

On considère un tableau de données T de taille n x m. Le tableau contient des informations sur une liste de N clients (avec N < n), où chaque ligne du tableau T[i] (i < N) correspond à la description d'un client différent (sur une trame de taille m).

1. Donnez la complexité des opérations suivantes:
   1. insertion d’un nouveau client
   2. recherche d’un client
   3. suppression d’un client
2. Donnez un algorithme permettant d’éviter l’insertion de doublons (On veut assurer que si i ≠ j, T[i] ≠ T[j]). Quelle est sa complexité?
3. Que faire pour accélérer les temps de recherche?
4. Que faire lorsque la page est pleine (n = N)?

On suppose maintenant que chaque tuple est désigné par sa « clé » k (entier). Un client est alors décrit par un tuple (clé, information₁, …, information_m). La clé k est unique : elle "identifie" le client.

On suppose ici que plusieurs tuples peuvent être enregistrés dans une même "page" i. Le tableau de données T est un "tableau de pages" où T[i] est la i^ème page du tableau.

En pratique, 2 grandes familles de méthodes d’accès sélectives (recherche par clé):

• méthodes d’accès par index : utilisation d'une table pour mémoriser l’association clé / adresse tuple : l'index est défini comme une série de couples ( (k₁, i₁), …, (k_N, i_N) ).
• méthodes d’accès par hachage : déterminent l’emplacement du tuple à partir d’une fonction de la clé,

1. Recherche par index
   1. Ecrire une fonction cree_index qui crée une liste associant à chaque clé le numéro de la page dans laquelle le tuple est enregistré.
   2. Quel est le temps nécessaire pour trier l'index sur les clés?
   3. Une fois l'index trié, quel est le temps nécessaire pour trouver un tuple dans le tableau de pages à partir de sa clé?
   4. Quel problème se pose lors de l'ajout de nouveaux tuples dans le tableau?
2. Table de hachage. Une table de hachage est une méthode d’indexation “automatique” dans laquelle l’index est remplacé par une fonction qui “décide” dans quelle page chaque tuple doit être rangé : si k est la clé du tuple, la fonction H(k) donne le numéro de la page où est stocké le tuple. Remarque : la taille du tableau est fixée à l’avance (p pages pouvant stocker n tuples)
   1. Quelle fonction H choisir pour répartir uniformément les tuples dans les cases?
   2. Donner l’algorithme qui remplit la table de hachage à partir d’un ensemble de N tuples et de p pages de taille n. Une fois la table créée, quel est le temps nécessaire pour savoir si le tuple de clé k est dans le tableau?
   3. Quel serait le nombre “idéal” de pages p pour stocker N tuples? En pratique, si on connaît N à l’avance, comment choisir au mieux p pour éviter que les cases “débordent”.
   4. Quels sont les avantages et les inconvénients de la table de hachage?
   5. Quelle structure de données Python, correspond à ce mode de stockage à base de clé ?
3. Index hiérarchique
   • Considérons un index composé de couples (clé, numero de page). On suppose que l’index est également découpé en pages, chaque page d'index contenant au maximum b clés. Si l’index comporte beaucoup de pages, il est intéressant de l’organiser hiérarchiquement en pages et sous-pages, selon une organisation appelée "B-arbre" (Balanced Tree):
     • chaque noeud de l’arbre contient une liste croissante de couples (clé, numéro d’une sous-page)
     • chaque clé est dupliquée dans sa sous-page :
       • les clés contenues dans la sous-page sont inférieures ou égales à elle,
       • les clés contenues dans la sous-page sont strictement supérieures à celles de la sous-page précédente.
       • les feuilles contiennent des couples (clé, numéro de la page du tableau de données)
   • On considère un ensemble de tuples stockés dans un tableau de données.
     • Le tableau de données est constitué de 10 pages numérotées de 201 à 210.
     • On considère également le tableau d’index permettant d’accéder plus rapidement aux données. Le tableau d’index est constitué de 4 pages numérotées de 101 à 104.
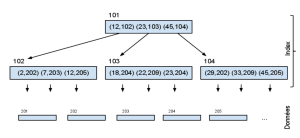
     • L’index est organisé de manière hiérarchique avec deux niveaux, comme indiqué sur le schéma suivant :

• a - Donnez l’algorithme qui, à partir d’une clé k, trouve le numéro de la page où est stocké le tuple correspondant.
• b - Sous quelle condition l’accès aux tuples sera-t-il efficace? Donnez dans ce cas le temps d’accès en fonction de b et du nombre de tuples N.