Table des matières
CM
1. Complexité(s)
- Complexité :
- Définition. intérêt.
- Complexité dans le cas le pire, le meilleur
- Complexité des algos récursifs (exemples : factorielle, coefficients binomiaux, tri par fusion)
- Complexité en moyenne (exemple du tri par insertion (simple) & de quicksort (un peu plus dur))
- Complexité minimales des pb (inversion de matrices en n^2, tri en n · log n, enveloppe convexe en n · log n)
- Introduction à la preuve de programmes ; exemple de l'algorithme d'Euclide.
- Présentation des Piles & Files d'Attente.
2. Graphes
3. Données non structurées
3.1 Données texte
3.1.1 Encodage des données
On distingue classiquement deux grandes catégories de données :
- données quantitatives:
- numérique entier ou réel, discrètes ou continues, bornées ou non. ex: poids, taille, âge, taux d’alcoolémie,…
- temporel : date, heure
- numéraire
- etc…
- données qualitatives:
- de type vrai/faux (données booléennes). ex: marié/non marié, majeur/non majeur
- de type appartenance à une classe. ex: célibataire/marié/divorcé/veuf, salarié/chômeur/retraité etc…
- de type texte (autrement dit “chaine de caractères”). ex: nom, prénom, ville,…
<!--
<note>
Parfois, la distinction entre quantitatif et qualitatif n’est pas nette:
* Possibilité d’ordonner les chaînes de caractères (de type nom/prénom) par ordre alphabétique
* On peut “traduire” une chaîne de caractères en entier (son code ASCII)
* Les valeurs logiques vrai/faux sont souvent traduites en valeurs “entières” 1/0
* Plus subtil : il est possible de définir des ordres partiels, des hiérarchies sur des données qualitatives :
* regroupement par secteur géographique
* notion de distance (géographique et temporelle) entre catégories
* Inversement, il est possible de rendre qualitatif des données quantitatives en réalisant des classes. Exemple : tranches d’âge 0-25/25-35/35-55/+55, mineur/majeur, recalé/passable/AB/B/TB etc...
</note>
--!>
Une valeur numérique (digitale) consiste en:
- un champ de bits (dont la longueur est exprimée en octets)
- un processus de décodage : le format (ou type)
- Les données manipulées par un programme:
- sont codées sous un format binaire,
- correspondant à un des types informatiques que vous connaissez déjà :
- entier,
- chaîne de caractères,
- réel simple ou double précision etc…
- ce qui implique en particulier :
- une précision finie,
- éventuellement des contraintes de place (le nom ou le prénom ne pouvant pas dépasser n caractères, les entiers pouvant être choisis sur un intervalle fini etc…).
<!--
<note>
**Types de données standards**
Les principaux types de données SQL sont les suivants :
* ''CHAR (longueur)'' : Ce type de données permet de stocker des chaînes de caractères de longueur fixe. ''longueur'' doit être inférieur à 255, sa valeur par défaut est 1.
* ''VARCHAR(longueur)'' : Ce type de données permet de stocker des chaînes de caractères de longueur variable. ''longueur'' doit être inférieur à 2000, il n'y a pas de valeur par défaut.
* ''TEXT'' : un texte de longueur quelconque
* ''INTEGER'' : entier (codage classique su 4 octets)
* ''NUMBER(longueur)'' : entier naturel, ''longueur'' précise le nombre maximum de chiffres significatifs stockés
* ''DECIMAL (longueur,[précision])'' : Le type de données decimal peut stocker jusqu'à 38 chiffres pouvant tous se trouver à droite de la virgule décimale. Il stocke une représentation exacte du nombre décimal, sans aucune approximation de la valeur stockée. ''longueur'' précise le nombre maximum de chiffres significatifs stockés (par défaut 38), ''précision'' donne le nombre maximum de chiffres après la virgule (par défaut 38), sa valeur peut être comprise entre -84 et 127. Une valeur négative signifie que le nombre est arrondi à gauche de la virgule.
* ''FLOAT'' : nombre à virgule flottante simple précision
* ''DOUBLE'' : nombre à virgule flottante double précision
* ''DATE'' : ce type de données permet de stocker des valeurs de type date. Format : '''2005-12-12''' (12 décembre 2005)
* ''TIME'' : ce type de données permet de stocker des valeurs de type heure. Format : '''10:45:02''' (10 h 45 min 2 s)
* ''DATETIME'' : donnée de type date-heure. Format : '''2005-12-12 10:45:02''' (12 décembre 2005, 10 h 45 m 02 s)
* ''TIMESTAMP'' : donnée de type date-heure (correspond à un stockage plus ‘compact’ que le type ''DATETIME'')
</note>
-->
3.1.2 Codage des caractères
x = 'a'
xune variable de type caractèreala valeur numérique (encodé):
-
- Codage ASCII :
- codage de symboles du clavier numérique.
- Le nombre de symboles étant inférieur à 256, on le code sur un octet : 2⁸ (= 256) valeurs différentes
- Codage UTF-8 :
- codage universel qui permet entre autre de coder les accents
- Codage latin-1 (caractères latins étendus)
- etc…
- le code ASCII code les caractères du clavier anglais sur 7 bits, ce qui permet d'interpréter chaque caractère comme un entier entre 0 et 127
- ainsi :
code = ord('/') print(code)
-
- affiche la valeur
47(le code ASCII du caractère'/')
- La norme UTF-8 encode les caractères sur un nombre d'octets variant entre 1 et 4. Il permet ainsi de coder un nombre de caractères considérablement plus élevé.
- Exemple : le smiley
'😃' appartient à la norme utf-8. Pour obtenir la valeur entière correspondante :
code = ord('😃') print(code)
- On peut inversement afficher le caractère à partir de son code entier :
print(chr(233)) print(chr(119070))
3.1.3 Codage des mots et du texte
Chaîne de caractère :
s = "bonjour"
sest une variable"bonjour"est une séquence de caractères- "chaîne" de caractères : type string en anglais
- assimilable à un tableau de caractère :
for c in s : print (c)
Affiche :
b o n j o u r
Le programme affiche les caractère 1 par 1, c’est une "chaîne" de plusieurs caractères individuels.
Donnée texte
Un texte, au même titre qu'un mot, est une chaîne de caractères (dont la longueur est définie par la longueur de la séquence de caractères qui définissent le texte, ponctuations, espaces et caractères de retour à la ligne compris).
Par définition les caractères séparateurs définissent la taille des espaces entre les mots, ainsi que les passages à la ligne lors de l'affichage du texte.
"": caractère nul" ": un espace simple"\t": tabulation"\n": passage à la ligne ("retour chariot")"\b": retour arrière ("backspace")- etc.
Codage du texte
L'ensemble des messages possibles peut être réduit à l'ensemble des entiers naturels. En effet, chaque caractère d'un texte peut être traduit en entier en interprétant le code binaire correspondant comme un entier.
Pour traduire une chaîne de caractères en entier, il faut "construire un nombre" à partir de chaque caractère de la chaîne en prenant en compte sa position.
- ainsi, dans le système décimal, la position du chiffre dans le nombre définit à quelle puissance de 10 il appartient (unité, dizaines, centaines, etc…) Le chiffre le plus à gauche a la puissance la plus élevée et celui le plus à droite la puissance la plus faible.
- Si on suppose, pour simplifier, que chaque caractère est codé par un entier entre 0 et 255 (soit le code ASCII "étendu"), alors toute séquence de caractères (de claviers européens) exprime un nombre en base 256.
- Un tel nombre s'appelle un "bytestring" en python.
- Il existe une fonction
encodequi effectue une telle traduction- Exemple :
s = 'paul.poitevin@centrale-marseille.fr' b = s.encode()
Un nombre en base 256 est difficile à lire et interpréter. On le traduit en base 10 :
i = int.from_bytes(b, byteorder='big') print("i =", i)
Ce qui donne :
i = 852806586114976881510056778471769180697471859150728801241505293627173168229624211058
3.1.4 Textes et bases de textes
- Bases de textes : ensemble constitué de plusieurs textes
- Bases de documents,
- Dossiers contenant des documents
- Collections de livres (électroniques)
- → 10 - 10⁴
- Contenus en ligne (descriptifs de films, articles de journaux, descriptifs de produits.)
- → 10⁵ - 10⁶
- Ensemble du web (les pages web, en tant que telles, peuvent être considérées comme du texte mis en forme par du html).
- → 10⁹
- Messageries, Blogs, Forums :
- 10³ - 10⁶
3.2 Recherche dans les textes
Exemples :
- → Recherche d’un terme : “artichaud”
- → Recherche d’un motif (expression régulière) : une adresse email, une URL, un expéditeur, un numéro tel
Problématiques de la recherche de texte :
- temps de réponse des algorithmes :
- l’utilisateur classique veut attendre moins de 2 à 3 secondes.
- Sur des bases extrêmement grandes (type recherche web), il faut donc être très performant pour atteindre ces temps de réponses.
- Stockage des données :
- intégralité des textes ou simple descriptif/résumé?
- Les moteurs de recherche par exemple ne stockent aucune page web, ils ne stockent que des index et des références.
Remarque :
Un document texte pourra être décrit soit comme :
- une séquence de caractères (lettres)
- une séquence de termes (mots)
3.2.1 Rechercher un terme
Recherche simple
d : document de taille m
On cherche un algorithme qui retourne toutes les occurrences (position dans le doc) d’un certain terme t (de taille k<m)
t = "ami"
d :
"Les amis de mes amis sont mes amis."
^ ^ ^
4 16 30
- → La position de la première occurrence du terme t :
- → Les positions de toutes les occurrences du terme t :
- Complexité : $O(m \times k)$
on note d le texte et t le motif recherché dans le texte
Algo : recherche_simple
Données : d, t : chaînes de caractères
Début
n = len (d)
m = len (t)
i <-- 0
tant que i < n - m:
j <-- 0
tant que j < m et d[i+j] = t[j] :
j += 1
si j == m :
retourner i
sinon :
i <-- i + 1
Fin
Remarque : Il peut être nécessaire de vérifier que le terme est précédé et suivi par les caractères d’espacement pour éviter de détecter les mots dont le mot recherché est préfixe ou suffixe.
Cette approche a un inconvénient : après une comparaison infructueuse, la comparaison suivante débutera à la position i + 1, sans tenir aucun compte de celles qui ont déjà eu lieu à l'itération précédente, à la position i.
Algorithme de Knuth-Morris-Pratt
L'algorithme de Knuth-Morris-Pratt examine d'abord la chaîne t et en déduit des informations permettant de ne pas comparer chaque caractère plus d'une fois.
- On suppose qu'on peut tester si un caractère
cappartient au motiften temps constant - Le but est de calculer un décalage permettant de ne pas inspecter les positions où il n'y a aucune chance de trouver le motif
t. - On commence par chercher la position
i = m - 1 - On inspecte la chaîne
ddeiài - mdécroissant, et on s'arrête au premier caractère commun (i.e.j⇐it.q.d[i-j]appartient àt) - Soit
c=d[i-j]le caractère commun - On note
kla position de la dernière occurrence decdanst[:m-j-1] - Le décalage est égal à
m - 1 - j - k - Si on ne trouve rien, le décalage vaut
m
RECHERCHE DE CHAINES CODEES EN MACHINE
CHINE
CHINE
CHINE
CHINE
CHINE
CHINE
CHINE
CHINE
CHINE
CHINE
RECHERCHE DE CHAINES CODEES EN MACHINE
Algo : recherche améliorée (Knuth-Morris-Pratt)
Données : d, t : chaînes de caractères
Début:
n = len (d)
m = len (t)
i <-- m - 1
tant que i < n :
# PRE-TRAITEMENT
j <-- 0
tant que j < m - 1:
c = d[i - j]
si c appartient à t[:m-j-1]
k <-- dernière_occurrence(c, t[:m-j-1])
decalage <-- m - 1 - j - k
break
sinon
j += 1
si j == m - 1:
decalage <-- m
# TRAITEMENT
j <-- 0
tant que j < m :
si t[m - j - 1] = d[i - j]
j += 1
sinon
break
si j = m:
retourner i - m + 1
# DECALAGE
i <-- i + decalage
retourner -1
Fin
3.2.2 Compter les mots
Lecture séquentielle des caractères :
"Les amis de mes amis sont mes amis." ^ position initiale de la tête de lecture
- Il ne faut compter que les debuts de mots
- Un début de mot est un caractère alphanumérique :
{a,à,ä,b,c,ç,d,e,é,è,ê,ë,...,z,A,B,C,...,Z,1,2,3,...,0}
- Tout ce qui n'est pas alphanumérique est un caractère séparateur
{!,#,$,%,&,",',...}
- Autrement dit on compte les couples (caractère séparateur, caractère alphanumérique)
- remarque : le début de chaîne compte comme un caractère séparateur
remarque : pour extraire la liste des mots présents dans le texte, on doit identifier les débuts et les fins de mots :
- un début de mot est un couple (sep., alphanum.)
- une fin de mot est un couple (alphanum., sep.)
Algo : compte-mots
Données :
- d : chaîne de caractères
Début:
nb_mots <-- 0
sep <-- Vrai
pour tout c dans d:
si sep est Vrai et c est alphanumérique:
sep <-- Faux
nb_mots <-- nb_mots + 1
sinon si sep est Faux et c est séparateur:
sep <-- Vrai
retourner nb_mots
Fin
Code équivalent : compter les mots à l'aide d'un automate fini:
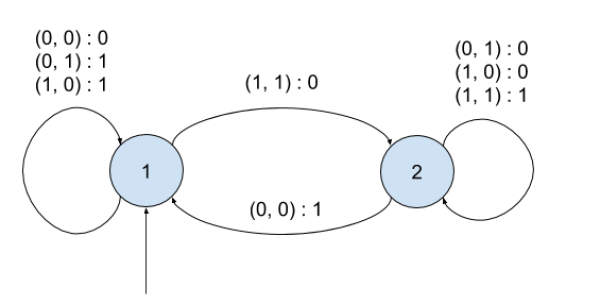
def compte_mots(d): state = 0 cpt = 0 for i in range(len(d)): if state == 0 and is_alpha(d[i]): state = 1 cpt += 1 if state == 1 and is_sep(d[i]): state = 0 return cpt
Présentation: un automate fini décrit les différentes étapes d'un calcul sous la forme d'un graphe orienté.
- les sommets du graphe sont les états. Un état identifie une étape de calcul. L'ensemble des états représente la mémoire (finie) de l'automate. Il existe un état initial, qui est celui dans lequel l'automate démarre au début du calcul.
- les arêtes représentent les transitions d'état. Un transition correspond à l'exécution d'un calcul élémentaire.
Pour réaliser des calculs, on a besoin d'opérandes. Les opérandes sont lus séquentiellement en entrée de l'automate. Ils obéissent à un certain alphabet (ou ensemble de symboles, …) $\Sigma$.
Enfin, des résultats de calcul sont produits en sortie de l'automate.
Plus concrètement, à chaque symbole lu en entrée, l'automate consulte une table des symboles acceptés à partir de l'état courant. Si le symbole est accepté, l'automate effectue la transition d'état, et produit une sortie (par exemple incrémenter le compteur de mots). Dans le cas contraire, il s'arrête.
Définition:
Un automate fini est défini par :
- un alphabet d'entrée $\Sigma$ (symboles acceptés)
- un alphabet de sortie $\Sigma$'
- un ensemble (fini) de sommets : $S$
- un ensemble fini d'arêtes : $A : S \times \Sigma \rightarrow S \times \Sigma'$ qui a tout couple (état, symbole d'entrée) associe un couple (état, symbole de sortie)
- un état initial $s_0 \in S$
L'état initial et la séquence des symboles lus définit la séquence de symboles produits en sortie (le résultat du calcul)
- $\Sigma = \{0, 1\}²$
- $\Sigma' = \{0, 1\}$
- $S = \{1, 2\}$
- $s_0 = 1$
La famille des automates finis définit une classe de calculs (l'ensemble des calculs réalisables par des automates finis):
- séquences
- boucles et branchements conditionnels
Mais pas :
- appels récursifs
remarque: il existe des automates de calcul plus puissants :
- automates à piles (calcul récursif)
- machines de Turing et machines de Turing universelles (calcul sur des automates)
permettant d'implémenter des calculs plus complexes
3.2.3 Recherche de motifs et expressions régulières
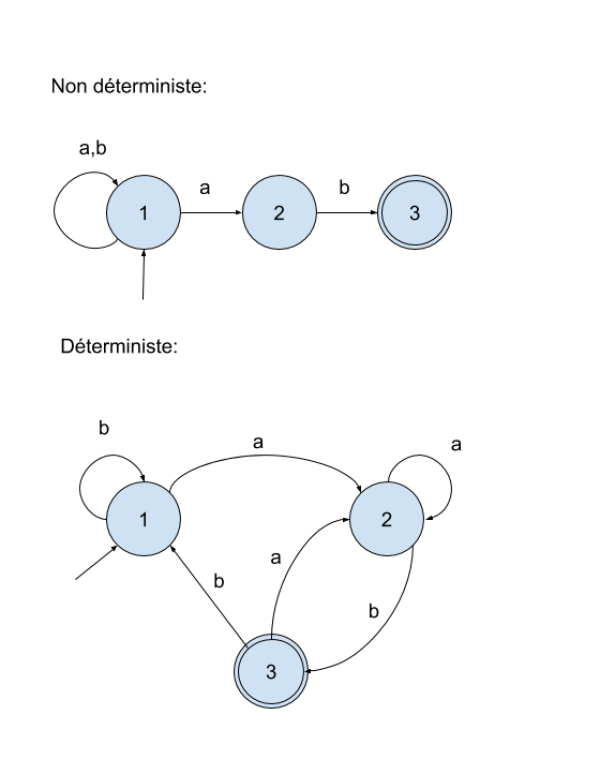
De manière plus générale recherche d’expressions peut être effectuée à l’aide d’automates finis non déterministes.
- Parmi les états on distingue les états initiaux et terminaux.
- Il existe (parfois) plusieurs transitions possibles pour un même symbole lu
- Lorsque l'automate s'arrête, on regarde si l'état est terminal. S'il est terminal, le mot est accepté (autrement dit le motif est "reconnu")
Remarque : pour tout automate fini non déterministe A, il existe un automate fini déterministe A′ qui reconnait le même langage (plus compliqué à écrire).
Représentation graphique :
- les états dans des cercles,
- l’unique état initial par une flèche pointant sur un état,
- les états terminaux par un double cercle concentrique sur l’état.
- Les transitions d’état quant à elles sont représentées par une flèche allant de l’état de départ jusqu’à l’état d’arrivée indexée par le caractère (ou le groupe de caractères) autorisant la transition.
Lecture séquentielle des caractères :
"Les amis de mes amis sont mes amis." ^ position initiale de la tête de lecture
- $\Sigma = \{a, b\}$
L'automate doit reconnaître les mots suivants :
ab bab abab bbab aabab abbab babab bbbab aaabab etc..
Exemples:
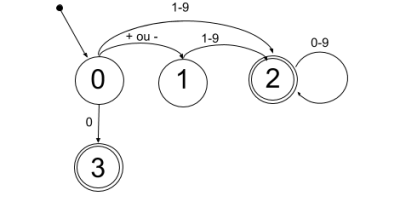
- Reconnaître un nombre entier :
+4,-455,1024,0
- Reconnaître un nombre réel :
- TODO
Remarques :
- Les classes d'expressions qui peuvent être reconnues par un automate fini sont appelées des expressions régulières
- En python, les expressions régulières s'expriment à l'aide d'une syntaxe spécifique à l'aide de la librairie
re
Traduction de l'automate non déterministe précédent sous forme d'expression régulière :
[ab]*ab
Remarque : les langages qui peuvent être reconnus par des expressions régulières sont appelés les langages réguliers.
Exemples de langages non réguliers:
- reconnaître les palindromes
- reconnaître une expression arithmétique
- vérifier la syntaxe d'un code informatique
Syntaxe des expressions régulières Python
Définition : Il s’agit d’une syntaxe “condensée” de description d’automates finis permettant de reconnaître des motifs dans un texte.
En Python, les expressions régulières sont implémentées dans la librairie re
import re d = "Les astronautes de la mission Gemini 8 sont désignés le 20 septembre 1965 : Armstrong est le commandant et David Scott le pilote. Ce dernier est le premier membre du groupe d'astronautes à recevoir une place dans l'équipage titulaire d'une mission spatiale. La mission est lancée le 16 mars 1966. Celle-ci est la plus complexe réalisée jusque-là, avec un rendez-vous et un amarrage du vaisseau Gemini avec l'étage de fusée Agena et une activité extravéhiculaire (EVA) qui constitue la deuxième sortie américaine et la troisième en tout, réalisée par Scott. La mission doit durer 75 heures et le vaisseau doit effectuer 55 orbites. Après le lancement de l'étage-cible Agena à 15 h 00 UTC, la fusée Titan II GLV transportant Armstrong et Scott décolle à 16 h 41 UTC. Une fois en orbite, la poursuite de l'étage Agena par le vaisseau Gemini 8 s'engage." liste_termes = re.findall(r"([1-9]\d*|0)", d)
Transitions : caractères et groupes de caractères
a: le caractère a[ab]: le caractère a ou le caractère b[a-z]: n'importe quel caractère minuscule entre a et z[^a]: n'importe quel caractère sauf le caractère a\n: le caractère "passage à la ligne".: n'importe quel caractère\.: le caractère "." uniquement[1-9]: un chiffre entre 1 et 9\w: n'importe quel caractère alphanumérique\s: n'importe quel caractère d'espacement\d: n'importe quel chiffre
Def : une expression est définie comme une suite de transition. Le mot est accepté lorsque la suite de transitions est respectée
Exemple :
r"chal[eu]t"
accepte chalet et chalut
r"\w\w\w"
accepte tous les mots de 3 lettres
Branchements et Récursion
- Les parenthèses permettent :
- de factoriser une expression (qui peut alors être traitée comme une transition)
(artichaud)
- de définir des branchements :
(chien|chat)
*: le caractère ou l'expression précédente répété entre 0 et n fois+: le caractère ou l'expression précédente répété entre 1 et n fois?: le caractère ou l'expression précédente répété entre 0 et 1 fois
exemples
- reconnaître une adresse mail :
r'\w[\.\w\-]*\w@\w[\.\w\-]*\.\w\w\w?'
3.3 Complétion / Correction
Un algorithme de complétion est un mécanisme logique permettant d'anticiper la saisie et de proposer des mots automatiquement pour faciliter les recherches dans un formulaire sur une page web par exemple.
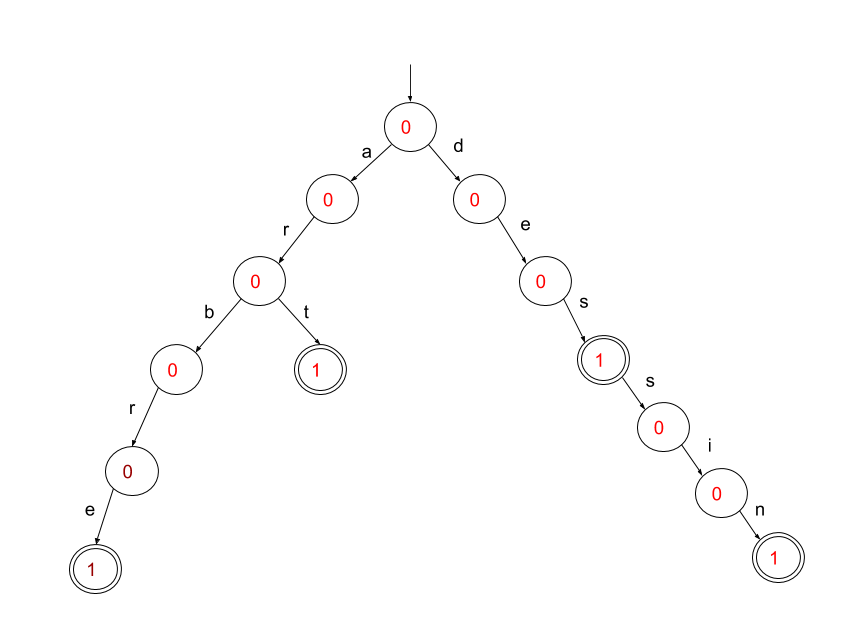
On utilise pour cela une structure de données arborescente, où chaque nœud de l'arbre est une étape de lecture et chaque arête correspond à la lecture d'une lettre. Les nœuds sont indexés par les lettres suivantes possibles du mot, avec un compteur par nœud pour savoir si celui-ci est final ou non (le nœud est final si le compteur est >0).
On commence par construire un arbre de complétion à partir de mots de vocabulaire,
L'arbre construit de cette manière est très large mais peu profond :
- Pour chaque nœud, le nombre de fils est de l'ordre de la taille de l'alphabet utilisé
- La hauteur maximale est celle de la taille maximale des mots de vocabulaire $n_{max}$
- Par construction, le nombre d'arêtes est borné par $|V|\times n_{max}$
Une fois l'arbre construit, on l'utilise pour compléter un début de mot proposé par l'utilisateur (souvent plusieurs complétions possibles).
Exemple :
- début de mot :
ar - complétions possibles :
{art, arbre}
3.4 Comparaison/appariement de textes
On cherche à exprimer une distance entre deux chaînes de caractères. Une distance entre 2 textes d1 et d2 est telle que :
- dist(d1,d2) = dist(d2,d1)
- dist(d1,d2) ≥ 0
- dist(d1,d2) + dist(d2,d3) ≥ dist(d1,d3)
Distance de Hamming
La distance de Hamming entre deux chaînes de même taille est définie comme le nombre de caractères non appariés. Ainsi la distance de Hamming entre "passoire" et "pastèque" est égale à 4.
Exemple :
p a s s o i r e | | | x x x x | p a s t e q u e
distance = 4
Peut-on généraliser cette distance à des chaînes de taille différente?
Distance d'édition
La distance d’édition est définie, pour deux chaînes de longueur quelconque, comme le nombre minimal d’opérations permettent de transformer d1 en d2, avec les opérations suivantes :
- ins(a) ⇢ insertion du caractère a
- perm (a, b) ⇢ remplacement de a par b
- del (a) ⇢ suppression du caractère a
Il existe différentes manières de transformer la chaîne d1 en d2. On peut par exemple supprimer tous les caractères de d1 et insérer tous les caractères de d2, mais c'est rarement le nombre d'opérations optimal (|d1|+|d2|).
- Exemples:
- distance entre "robe", "arbre", et "porte".
- r o b - e v | ^ | v | a r - b r e
dist = 3
r o b - e x | x v | p o r t e
dist = 3
a - r b r e x v | x ^ | p o r t - e
dist = 4
Calcul complet cloche/hochet
La résolution de ce problème repose sur les principes de la programmation dynamique.
Un problème d'optimisation combinatoire se caractérise par :
- un problème
- un ensemble de solutions à ce problème
- une fonction de coût (ou une fonction objectif) qui attribue un coût (resp un gain) à chacune des solutions possibles apportées au problème
Le nombre de solutions possibles à un problème d'optimisation combinatoire croît exponentielleemnt avec la taille du problème. Trouver une solution par énumération à un tel problème devient rapidement impossible pour des problèmes de taille modérée.
Certains problèmes d'OC peuvent être résolus selon le principe de la programmation dynamique qui consiste à décomposer le problème en sous-problèmes (et en sous-solutions):
- soit un problème P présentant une solution S de coût C
- Étant donné un sous problème $p \subset P$,
- on liste l'ensemble des sous-solutions $s, s', s''$ applicables à p
- et on sélectionne celle dont le coût est le plus faible
- on modifie S selon la sous-solution sélectionnée
- on met à jour le coût global
- on met à jour le sous-problème
- et on recommence jusqu'à la convergence (p = P)
Dans le cas de l'appariement de chaîne:
- une solution est un ensemble de transformations acceptables pour passer de la chaîne A à la chaîne B
- le coût est la somme des coûts des transformations appliquées
- un sous-problème consiste à apparier un morceau de A avec un morceau de B
En pratique:
- on représente l’ensemble des transformations de d1 vers d2 sous la forme d’un tableau de (m + 1) lignes et (n + 1) colonnes, avec m = |d1| et n = |d2|
- pour chaque case (i,j) du tableau,
- le passage vers la case (i, j+1) correspond à ins(d2[j])
- le passage vers la case (i+1, j) correspond à del(d1[i])
- le passage vers la case (i+1, j+1) correspond à perm(d1[i],d2[j]) ou id(d1[i],d2[j]) si d1[i]=d2[j]
- la valeur de la distance au niveau de la case (i,j) est égale au minimum de :
- 1 + dist(i, j+1)
- 1 + dist(i+1, j)
- dist(i+1, j+1) si d1[i]=d2[j], ou 1 + dist(i+1, j+1) sinon
- la distance au niveau de la case (m,n) vaut 0
- la distance d'édition est donnée par la valeur dans la case (0,0)
Algorithme
Préparation
variables globales : d1, d2 : chaînes de caractères m = |d1| n = |d2|
Récursif!!
algo : distance
données :
i, j : etape de calcul
début
si i = m et j = n :
retourner 0
sinon si i = m :
retourner dist(i, j+1) + 1
sinon si j = n :
retourner dist(i + 1, j) + 1
sinon si d1[i] = d2[j] :
retourner min(dist(i, j+1) + 1, dist(i + 1, j) + 1, dist(i + 1, j + 1))
sinon
retourner min(dist(i, j+1) + 1, dist(i + 1, j) + 1, dist(i + 1, j + 1) + 1)
fin
Alignement glouton
4. Fichiers et indexation
- Il s'agit par définition des informations qui doivent être conservées entre deux exécutions.
- Avec l’augmentation des capacités de stockage et leur mise en réseau, les quantités de données conservées ont considérablement augmenté au cours des dernières décennies.
Dans le cadre de ce cours, nous aborderons :
- la question du stockage de ces données sur un support informatique (Fichiers, bases de données),
- ainsi que les méthodes permettant de consulter et mettre à jour régulièrement ces données.
4.1 Données et fichiers
4.1.3 Transport et flux de données
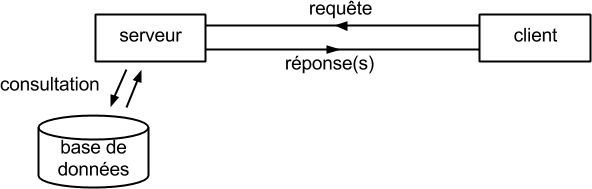
- La transmission des données entre programmes nécessite l’ouverture d’un canal de communication
- entre client et serveur
- par lequel transitent les données (les requêtes et les réponses).
- Le transport est géré
- par le système d’exploitation (lorsque les données transitent au sein d’un même ordinateur)
- ainsi que par des routeurs (lorsque les données transitent d’un ordinateur à l’autre sur le réseau).
- Au niveau du client,
- les réponses en provenance du serveur sont organisées sous la forme d’une liste,
- qu’on appelle un flux de données.
Formats d'échange
Les principaux formats d'échange de données sont :
- csv
- json
- xml
Exemples :
4.1.4 Conservation des données
La conservation des données repose principalement sur la structure de stockage,
- définissant la manière dont les données sont physiquement stockées sur le support,
- autrement dit la méthode de rangement de la série de mesures :
- fichiers,
- répertoires,
- index,
- etc…
- reposant sur des supports de stockage (ou mémoires) :
- mémoire centrale,
- mémoires secondaires (disque dur, CD-ROM, memoire flash (SSD), etc…).
Trame et bloc de données
Un jeu de valeurs encodé et stocké sur un support informatique est appelé un “enregistrement”,
- conservé sous la forme d'une trames de données.
- Une trame peut obéir à un format textuel ou binaire
Encodage binaire :
- Définition d’une trame, en général de taille fixe.
- Chaque rubrique occupe un nombre d’octets déterminé, afin que chaque jeu de données occupe la même place en mémoire.
- L’utilisation de trames de taille fixe facilite le stockage et la conservation des données sur les supports magnétiques (disque dur, etc…)
- Les données sont transmises dans un format numérique (type) identique à celui utilisé en mémoire centrale.
Encodage textuel :
- Le jeu de données est codé dans un format descriptif (contenant à la fois les valeurs et une description des données : types, attributs, …).
- Ce format facilite la transmission d’un programme à un autre (format “plat”) mais est moins propice au stockage.
- La “sérialisation” est l’opération qui consiste à encoder des données sous la forme d’un texte brut (codage ASCII ou utf8), en “perdant” le moins possible d’information.
- Des exemples de formats textes standards sont donnés en 2.1.3 Structures de données.
Tableaux statiques
Bloc de données
Un bloc de données correspond à une série d’enregistrements obéissant au même format:
- Chaque enregistrement est de taille identique;
- L'encodage des données est le même.
La structure de base servant à stocker à une série d’enregistrements est le tableau de données à 2 dimensions :
- Tableau de données (data frame) = intitulé de colonnes + liste de lignes
- Intitulé de colonne = nom de l’attribut
- Une ligne = un enregistrement
Structure sous-jacente : tableau à 2 dimensions (ou matrice de données)
Tableau statique
Un bloc de données obéit formellement à une structure de type tableau statique:
- Un tableau statique est une structure séquentielle de taille fixe, constituée de $N$ "cases"
- Les cases peuvent être "libres" ou "occupées".
- taille limitée du support matériel
- données accessibles grâce à leur adresse (position dans le tableau)
- problème de rangement (il faut conserver une information sur la position des données déjà enregistrées) ⇒ organisation logique des données sur le support.
- Dans un tableau statique
T, la position des cases reste fixe au cours de l'utilisation :T[i]désigne toujours la mếme zone mémoire
- Dans un tableau dynamique (liste python par exemple), la position des cases varie au cours de l'utilisation :
T[i]ne désigne pas toujours la mếme zone mémoire- Analogie : briques de lego, puzzle glissant
Structure de stockage
Les mémoires informatiques sont des structures statiques. Une fois les données sauvegardées sur le disque, il est difficile d’insérer ou de supprimer des éléments.
La difficulté consiste à définir une organisation logique du tableau permettant de gérer efficacement un tel ensemble (qui peut être de grande taille) :
- savoir où enregistrer les données
- savoir comment les retrouver
On parle de structure de stockage. Une telle structure doit permettre :
- d’ajouter des données
- d'effacer des données
- d’accéder rapidement à une case particulière
Stockage dense
On considère un ensemble de k données stockés dans un tableau de données statique T de N cases (avec 0≤k ≤ N).
Remarques :
- Les cases du tableau sont numérotées de
0àN-1 - Les données sont de type quelconque mais chaque case ne peut contenir qu'une donnée
- Si
iest un indice de case,T[i]désigne le contenu de la case Nest fixé maiskvarie en fonction du nombre de données stockées
Propriété : les données sont stockés dans les k premières cases du tableau. Ainsi, les cases de 0 à k-1 sont occupées et l'indice k désigne la première case libre.
Opérations fondamentales :
- insertion de données : O(1)
- recherche de données : O(k)
- suppression de données : O(k)
Stockage distribué
On conserve une table des cases libres
- Index bitmap :
- Chaque bit correspond à une case (libre/occupé).
- Lors de l’écriture d'une nouvelle donnée (allocation), on fait passer le bit de 0 à 1
- Lorsque la donnée est effacée, le bit correspondant passe de 1 à 0
$$B = \underset{0}{0}{10010100100.....}\underset{n-1}{01}$$
- Table d'allocation:
- On considère un tableau de taille $n$ dans lequel $k < n$ cases sont occupées.
- Chaque bloc de données $d$ est indexée par l'adresse $i < n$ donnant sa position dans le tableau
- On connaît également sa taille $m$.
- La table d'allocation donne pour chaque bloc :
- sa position $i$
- le nombre $m$ de cases occupées
Stratégies d’allocation
Stratégie par bloc: on alloue des blocs composés de plusieurs cases (S’il existe des blocs libres consécutifs, ils sont fusionnés en un seul)
On souhaite :
- minimiser le nombre de blocs libres
- maximiser la taille des blocs libres
- Plus proche choix : la liste des blocs libres est parcourue jusqu’à trouver un bloc de la taille demandée (ou sinon, le premier bloc de taille supérieure, qui est alors découpé en deux blocs).
- first fit : le premier bloc suffisamment grand pour les besoins
- best fit : le plus petit bloc qui ait une taille au moins égale à la taille demandée
- worst fit : le plus grand bloc disponible (qui est donc découpé)
Écrire un algorithme permettant d'insérer une donnée $d$ de taille $m$ dans le premier bloc libre disponible (pensez à mettre à jour la table d'allocation $B$).
Autre stratégie (allocation rapide): On alloue des blocs de 1,2,4,8,…2K pages. Pour une taille donnée 2i-1 < n < 2i, on commence par chercher les blocs de taille 2i, puis 2i+1, … jusqu’à 2K , en divisant ces blocs le cas échéant.
Problème des stratégies par bloc: s’il y a trop de données, on obtient des blocs de taille 1 –> nécessité de réorganiser (défragmenter)
4.1.5 Fichiers et répertoires
La mémoire secondaire n’est pas directement accessible (les programmes n’ont pas la possibilité d’aller écrire directement sur le disque). Le système d’exploitation assure ainsi l’indépendance du programme par rapport à l’emplacement des données, au travers d’instructions d’entrée/sortie spécialisées.
Pour que les programmes puissent écrire sur le disque, on introduit des objets intermédiaires : les fichiers. Un fichier est caractérisé par (nom, emplacement (volume, arborescence), droit d’accès, taille,…). Il s’agit d’une entité logique. Tout programme utilisant un fichier passe par le système d’exploitation qui, à partir des informations, détermine la localisation des données sur le support.
- Un fichier est une référence vers un ou plusieurs blocs de données, enregistrés sur un support physique.
- Un fichier est caractérisé par son descripteur, constitué de son nom, son chemin d’accès, ses droits d’accès (lecture/écriture/exécution) selon les utilisateurs, sa position sur le support, sa taille, etc…
- La gestion des fichiers est une des fonctions essentielles des systèmes d’exploitation :
- possibilité de traiter et conserver des quantités importantes de données
- possibilité de partager des données entre plusieurs programmes.
- Ouverture : initialisation d'un flux en lecture ou en écriture
- Lecture : consultation des lignes l'une après l'autre (à partir de la première ligne), dans l'ordre où elles ont été écrites sur le support
- Ecriture : ajout de nouvelles données à la suite ou en remplacement des données existantes
Le volume est le support sur lequel sont enregistrées les données. On parle de mémoire secondaire (Disque dur, disquette,CD-ROM, etc…). Un volume est divisé en pistes concentriques numérotées de 0 à n ( par ex n = 1024). Chaque piste supporte plusieurs enregistrements physiques appelés secteurs, de taille constante (1 secteur = 1 page).
Page (ou secteur)
Les pages sont les unités de base pour la lecture et l'écriture. une page est une zone contiguë de la mémoire secondaire qui peut être chargée en mémoire centrale en une opération de lecture. Taille standard : une page = 1-2 ko.
La mémoire secondaire est donc organisée comme un tableau de pages : (T[0],…,T[L-1]), où L est le nombre de pages. Chaque page fait m octets. Chaque page peut être libre ou occupée.
Répertoires Chaque volume possède un numéro appelé le label du volume. Tous les descripteurs de fichiers sont regroupés dans une table des matières appelée Répertoire (Directory).
Remarque : cette table des matières est en fait un fichier dont le descripteur est contenu dans le label du volume.
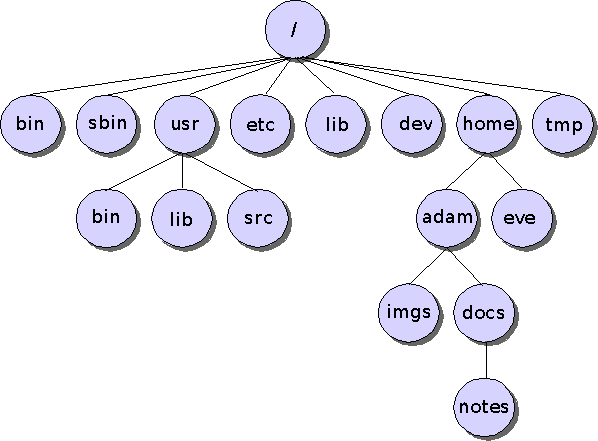
Organisation hiérarchique :
- Lorsque le nombre de fichiers est élevé, les descripteurs de fichiers sont classés dans plusieurs répertoires, organisés sous une forme arborescente.
- Le répertoire de plus bas niveau hiérarchique est appelé racine → chemin d’accès (path)
Consultation des données : lecture d’un fichier (Read)
Méthode traditionnelle pour le traitement de fichiers de petite taille. La consultation des données nécessite d’ouvrir une “communication” entre le programme et les fichiers. Ce canal de communication permet de recevoir un flux de données.
Pour établir la communication, il faut connaître : le “chemin d’accès” aux données (disque dur local) l’”adresse” des données (lorsqu’il s’agit de données stockées sur un serveur distant)
L’opération d’ouverture de fichier initialise un descripteur de fichier, qui sert à désigner (dans le programme) le fichier sur lequel on travaille, et d’accéder au contenu du flux.
Ouverture simple:
f = open('/chemin/vers/mon/fichier.dat','r')
Le deuxième argument représente le mode d’ouverture, ici ’r’ représente une ouverture en mode lecture.
Ouverture avec test :
Il est important de vérifier que cette opération d’ouverture s’effectue correctement avant de poursuivre le programme (nombreuses possibilités d’erreur : fichier effacé, erreur de nom, pas de droits de lecture,…).
On utilise une instruction de test spécifique pour vérifier que l’ouverture du fichier s’est correctement effectuée, de type try…catch… (essaye … sinon …) permettant de prévoir une action de secours lorsqu’une une opération “risquée” échoue.
try :
f = open('/chemin/vers/mon/fichier.dat','r')
except IOError:
print "Erreur d'ouverture!"
Lorsque l’opération d’ouverture est réalisée avec succès, le flux de données devient accessible en lecture (les premières lignes du fichier sont chargées en mémoire et une tête de lecture se positionne sur le premier caractère de la première ligne). Il ne reste plus qu’à lire les données.
La consultation des données s’effectue séquentiellement à l’aide de l’opérateur de lecture readline. Chaque appel à cet opérateur charge les nouvelles données et déplace la tête de lecture vers les données suivantes. Cette opération peut être effectuée plusieurs fois jusqu’à atteindre la fin de fichier.
Remarque : Lecture/Ecriture
Les opérateurs lire_ligne (readline) et écrire_ligne (write) ne travaillent pas directement sur les données du fichier. Les données du fichier sont chargées en mémoire centrale dans une mémoire “tampon”. L’objet f servant à décrire le fichier a comme attributs :
- t : table des pages,
- i : numero de la page courante,
- p : tableau d'octets de la page courante (mémoire tampon),
- j : position dans la page courante (tête de lecture).
Lors des opération de lecture, la mémoire tampon est mise à jour au fur et à mesure qu’on avance dans la lecture du fichier par des opérations de lecture sur le disque. En général, plusieurs pages sont chargées en avance. Lors d’une opération d’écriture, la mémoire tampon reçoit les nouvelles données à écrire. Ces données sont effectivement écrites sur le disque lorsque le tampon est suffisamment rempli ou lors de l’opération de fermeture. Au moment de l’écriture effective, le système d’exploitation fait appel à un opérateur d’allocation pour choisir le “meilleur” bloc où stocker les données.
Si on suppose que les données sont rangées sous la forme d’un tableau de lignes, chaque opération de lecture consiste à consulter une ligne du tableau, et à positionner la tête de lecture sur la ligne suivante.
1. Lecture d’une ligne unique :
Python
s = f.readline()
2. Lecture de toutes les lignes (la lecture s’effectue dans une boucle) + affichage de la ligne:
Python
for s in f : print s
Enregistrement des données : sauvegarde dans un fichier (Write)
L’opération de sauvegarde des données est l’opération complémentaire de la lecture. De nouvelles données doivent être enregistrées sur le disque dur en vue d’une consultation future. Le format de sauvegarde peut être de type texte ou de type binaire. Nous présentons ici la sauvegarde des données dans des formats texte.
Comme dans le cas de l’opération de lecture, il faut au préalable définir dans le programme un descripteur de fichier servant de point d’entrée pour les opération d’écriture. On effectue ce qu’on appelle une ouverture en mode “écriture”.
Python
try :
f = open('monfichier.dat','w')
except IOError:
print "Erreur d'ouverture!!"
On notera qu’il existe en python (ainsi qu’en C, C++, …) plusieurs modes d’ouverture exprimés par le deuxième argument de la fonction open. On retiendra le mode ‘w’ (création d’un nouveau fichier vide) et le mode ‘a’ (ajout de nouvelles données à la suite d’un fichier déjà existant).
La sauvegarde dans le fichier s’effectue à l’aide d’un opérateur d’écriture. Dans le cas des chaînes de caractères, l’opérateur d’écriture sauvegarde ces données à la suite des données déjà écrites.
Python
f.write("Bonjour!\n")
La sauvegarde de données nécessite d’effectuer un choix sur le mode d’encodage, obéissant en général à une norme bien précise (csv, json, xml, etc…). Voir section 1.3.
Une fois les opérations de lecture ou d’écriture terminées, il est nécessaire de fermer le fichier. L’opération de fermeture assure que les données sont effectivement enregistrées sur le disque (et non simplement stockées dans la mémoire tampon - voir section XXX).
Voir aussi :
4.2 Index et Données
Une donnée informatique est un élément d'information ayant subi un encodage numérique
- Consultable/manipulable/échangeable par des programmes informatiques
- Possibilité de la conserver sur un support de stockage numérique (CD-ROM, disque dur, SSD, …)
- Les informations peuvent être stockés dans un fichier (ex : fichier csv).
- Un jeu de valeurs encodé et enregistré est appelé un enregistrement
Pour une gestion efficace des données, il est nécessaire de pouvoir identifier chaque enregistrement de façon unique.
L'indexation des données repose sur un principe simple d'étiquetage consistant à attribuer une étiquette différente à chaque enregistrement. Cette étiquette peut être une suite de caractères arbitraires, un entier, ou un descripteur explicite. On parle en général de clé ou d'identifiant pour désigner cette étiquette.
4.2.1 Définitions et propriétés
- L'indexation des données consiste à attribuer à chaque donnée distincte un identifiant unique.
- On parle également de clé de l'enregistrement:
On peut représenter l'opération d'indexation sous la forme d'une fonction. Si $d$ est le jeu de valeurs, $k(d)$ désigne l'identifiant de ce jeu de valeurs.
Unicité/spécificité
L'indexation suppose l'existence d'une bijection entre l'ensemble des données et l'ensemble des clés, permettant d'assurer l'unité et la spécificité de la clé
- soient $d_1$ et $d_2$ deux enregistrements,
- Unicité :
- si $d_1 = d_2$, alors $k(d_1)=k(d_2)$.
- Spécificité:
- si $k(d_1) = k(d_2)$, alors $d_1=d_2$.
Efficacité
L'existence d'un identifiant unique pour chaque jeu de valeurs $d$ permet la mise en œuvre d'une recherche par identifiant (ou recherche par clé).
La recherche par identifiant repose sur une fonction d'adressage $I$ qui à tout identifiant $k$ associe sa position (entrée) $i$ dans un tableau de données: $I : k \rightarrow i$. Ainsi si $k$ est l'identifiant servant à la recherche, l'extraction des informations se fait en 2 étapes:
- $i = I(k)$ (lecture de l'index des données)
- $d = D[i]$ (lecture des données elles mêmes)
Compacité
L'identifiant doit en pratique tenir sur un nombre d'octets le plus petit possible pour que la liste $L$ puisse être manipulée en mémoire centrale. Autrement dit, il faut que :
- $|k| << |d|$
pour que :
- $|L| << |D|$
4.2.2 Utilisation
Définir un ordre sur les données
La présence d'un identifiant permet de définir un ordre total sur les données :
- ordre sur les entiers (identifiant entier)
- ordre alphabétique (identifiant texte)
- ordre ASCIIbétique (chaîne de caractères quelconque)
Lier les données
Dans le cas des bases de données, l'identifiant constitue une référence vers les jeux de valeurs des tableaux de données. Une référence permet de lier les données d'une table aux données d'une autre table.
Exemple :
- Pour chaque album de la table des albums, l'identifiant d'artiste (ici un numéro) permet de lier l'album avec l'artiste (ou groupe) correspondant.
- Pour chaque piste de la table des pistes, l'identifiant d'album permet de lier la piste à l'album correspondant (et donc à l'artiste correspondant par transitivité)
Structure d'ensemble
L'index définit l'appartenance d'une donnée à un ensemble.
Soit $\mathcal{E}$ un ensemble de données indexées : $$ \mathcal{E} = \{d_1, d_2, ..., d_K\} $$ On a l'équivalence : $$ d \in \mathcal{E} \Leftrightarrow k(d) \in I $$
Ainsi, il ne peut y avoir de doublon car $\forall d$ :
- $k(d)$ est unique
- $i = I(k(d))$ est unique ssi $d \in \mathcal{E}$ et indéfini sinon.
4.3 Exemples d'indexation des données
4.3.1 Adressage des tableaux
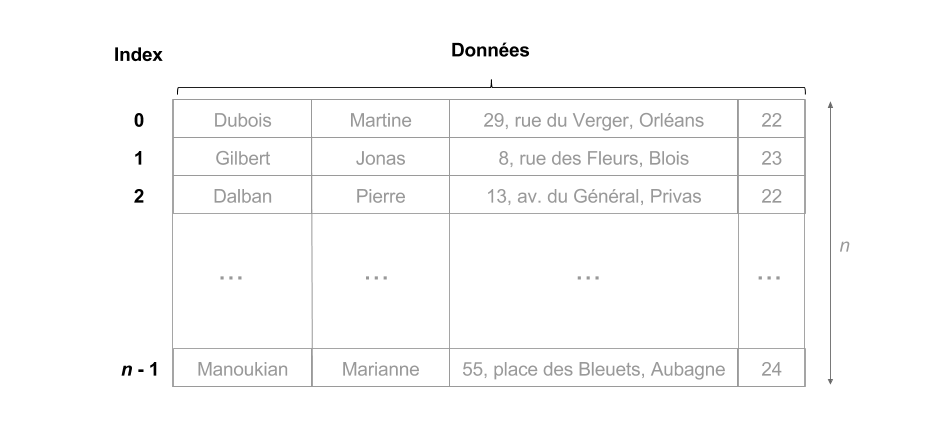
L'exemple le plus simple d'indexation est celui fourni par les numéros de case d'un tableau.
- Soit $D$ un tableau de $n$ lignes
- le numéro $i < n$ est à la fois l'identifiant et l'entrée (ou adresse) de la ligne $D[i]$
4.3.2 Maintenance centralisée d'un index
Dans le cas général, l'identifiant n'est pas égal à l'entrée!
On sépare donc l'index $k$ de l'entrée $i$:
- $k$ est l'identifiant (ou clé) de la donnée $d$. Il s'agit d'une valeur numérique quelconque.
- $i$ est l'entrée de la donnée $d$, correspondant à sa position dans le tableau de données.
- l'intégrité de l'index
- l'unicité de l'identifiant
Il existe différentes méthodes permettant d'assurer l'intégrité de l'index:
- Le programme maintient une liste triée des identifiants déjà utilisées. Lors de l'ajout d'une nouvelle donnée, il s'assure que l'identifiant n'est pas déjà présente dans la liste.
- Coût :
- $O(n)$ en mémoire
- $O(\log n)$ pour l'ajout
- Dans le cas où les identifiants sont des numéros (entiers), il est possible d'utiliser un compteur qui s'incrémente à chaque nouvelle insertion.
- Coût :
- $O(1)$ en mémoire
- $O(1)$ pour l'ajout
- numéro INE (étudiants)
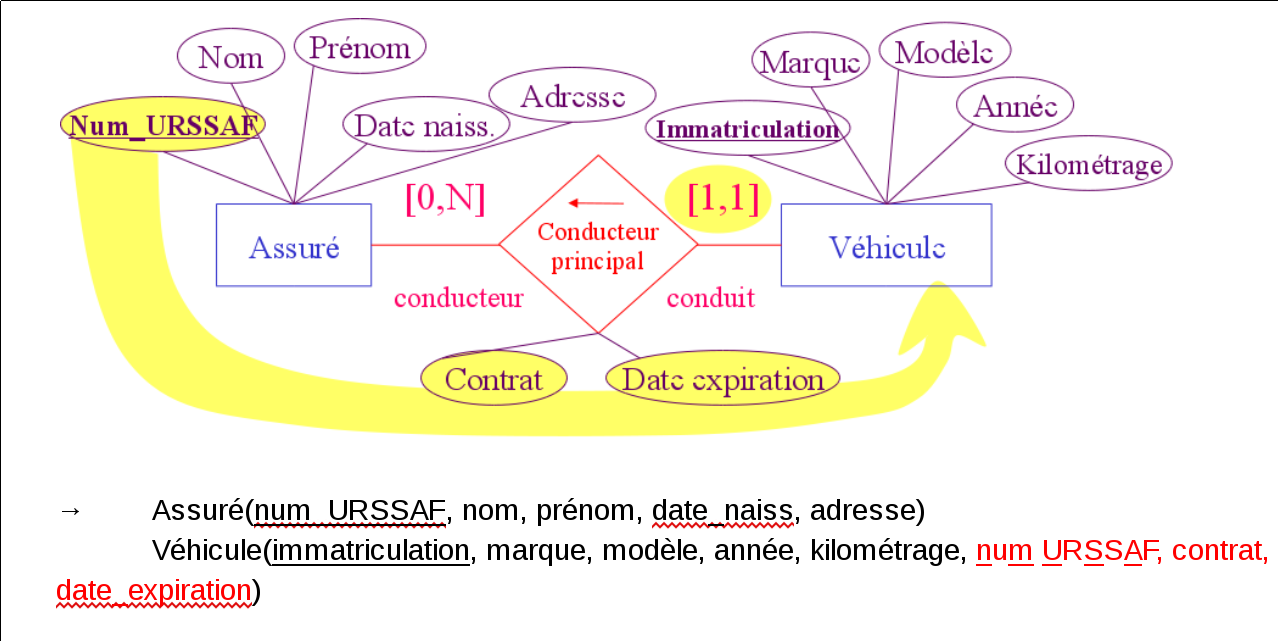
- numéro URSSAF (sécurité sociale)
- numéro d'immatriculation (véhicules)
- numéro de compte en banque
- code barre
- etc.
4.3.3 Indexation pseudo-aléatoire : les fonctions de hachage
Utilisation d'une fonction de hachage :
- qui "calcule" la valeur de l'identifiant à partir des valeurs du jeu de valeurs à insérer.
- La fonction de hachage doit être telle que la probabilité de choisir le même identifiant pour deux données différentes soit extrêmement faible.
Attribution d'un identifiant arbitraire entre 0 et n-1
- Etape 1 : transcodage binaire des données
i = int.from_bytes(d, byteorder='big')- avantage : les données différentes ont un code entier différent
- mais : |i| = |d|
s = 'paul.poitevin@centrale-marseille.fr' d = bytes(s, 'ascii') i = int.from_bytes(d, byteorder='big') print("i =", i)
donne :
i = 852806586114976881510056778471769180697471859150728801241505293627173168229624211058
- Etape 2 : réduction du code
- Méthode 1 : le modulo n (reste de la division entière par n)
k = H(i) = i mod n- Avantage :
- $|k| << |d|$
- Inconvénient:
- deux données différentes peuvent avoir le même code
- ce codage revient à sélectionner les bits de poids faible
- deux données proches ou très similaires auront un index proche ou similaire : si
j = i + 1,H(j) = H(i) + 1(presque toujours) - —> il faut prendre n premier
-
-
- $n = 2^{32} = 4294967296$ :
- H_code(
paul.poitevin@centrale-marseille.fr) =1697539698 - H_code(
martin.mollo@centrale-marseille.fr) =1697539698
- $n = 67280421310721$ (premier):
- H_code(
paul.poitevin@centrale-marseille.fr) =36148249469507 - H_code(
martin.mollo@centrale-marseille.fr) =65330032132071
-
-
- Méthode 2 : combiner produit et modulo – soient m et n deux nombres premiers entre eux
k = H(i) = (i * m) mod n- Avantage :
- $|k| << |d|$
- deux entiers proches donneront auront des codes très différents : si
j = i + 1,j * m - i * m = m
- Inconvénient :
- deux données différentes peuvent avoir le même code
- le produit
i * mpeut etre coûteux à calculer
- Méthode 3 : Hachage cryptographique :
- Le hachage cryptographique est construit de telle sorte qu'il soit très difficile de trouver un entier
j != itel queH(i) = H(j). - Un tel code est appelé une "signature".
- Exemples :
Exemple
Le gestionnaire de bases de données MongoDB utilise une indexation des données par clé cryptographique.
4.4 Généralisation : multi-indexation
4.5 Structures de données pour l'indexation
4.5.1 Liste triée
4.5.2 Index bitmap
4.5.3 Les B-arbres
Que faire lorsque l'index ne tient pas en totalité dans la mémoire centrale ?
- L'index est découpé en "blocs"
- Les blocs sont organisés sous la forme d'un arbre (B-arbre = "Balanced Tree")
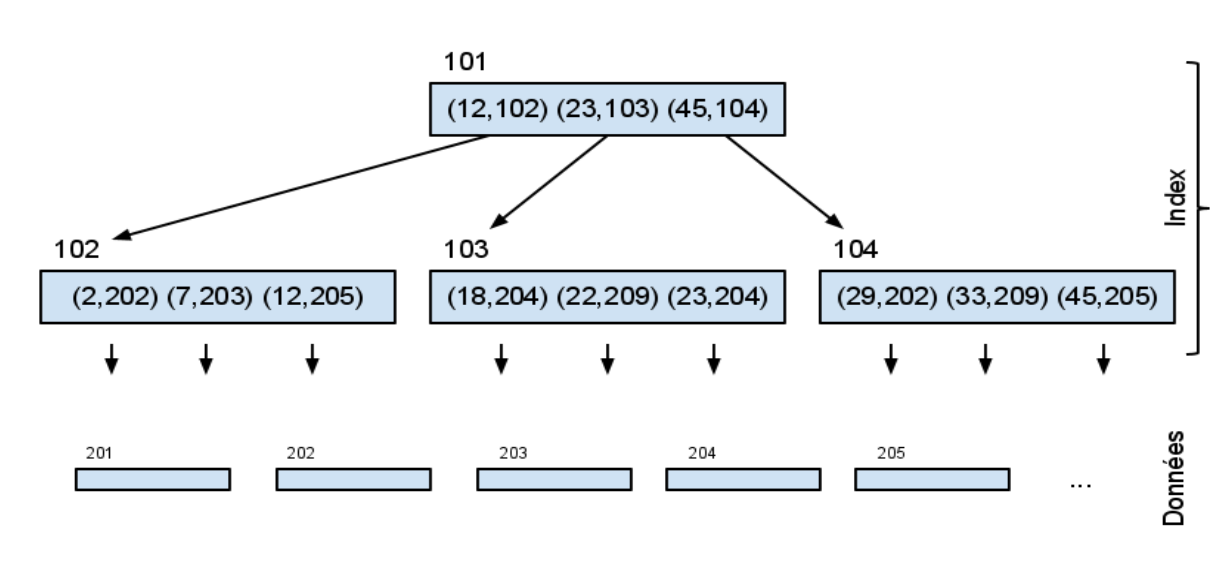
Considérons un index composé de couples (clé, numero de page). On suppose que l’index est également découpé en pages, chaque page d'index contenant au maximum b clés. Si l’index comporte beaucoup de pages, il est intéressant de l’organiser hiérarchiquement en pages et sous-pages, selon une organisation appelée "B-arbre" (Balanced Tree):
- chaque noeud de l’arbre contient une liste croissante de couples (clé, numéro d’une sous-page)
- chaque clé est dupliquée dans sa sous-page :
- les clés contenues dans la sous-page sont inférieures ou égales à elle,
- les clés contenues dans la sous-page sont strictement supérieures à celles de la sous-page précédente.
- les feuilles contiennent des couples (clé, numéro de la page du tableau de données)
- paramètre d’entrée : k
I ← charger la racine de l’arbre
tant que I n’est pas une feuille :
k’ ← première clé de I
tant que k > k’
k’ ← clé suivante
I ← charger sous-page de k’
Remarque : Pour que l’accès aux données soit efficace,
- il faut que l’arbre soit le moins profond possible : arbre “équilibré”.
- Dans ce cas,
- chaque noeud a
bfils, - et la profondeur de l’arbre est de l’ordre de logb(N).
- Pour charger la page contenant le tuple cherché,
- il faut donc logb(N) + 1 lectures sur disque.
En pratique, il existe des algos permettant d’assurer que chaque noeud contient entre b/2 et b clés (sauf la racine).
5. TODO
6. Bases de données relationnelles
On introduit dans ce chapitre le modèle relationnel qui sert de fondation à la conception de bases de données.
Les différents modèles utiles en représentation des connaissances reposent sur des notions de base de la théorie des ensembles :
- Ensemble finis
- Éléments partiellement (ou totalement) discernables
6.1 Structures de données
6.1.1 Production des données
Tout commence par une fiche à remplir…
- Un formulaire se présentant sous la forme d’un ensemble de rubriques à remplir.
- Le modèle de fiche définit le format des données à enregistrer:
- liste des rubriques du formulaire,
- domaine de valeurs attendues dans chaque rubrique.
- A toute fiche remplie correspond un jeu de valeurs (ou mesure) :
- liste de valeurs correspondant au contenu d’une fiche particulière.
- une personne réelle : assuré, client, étudiant, auteur, plaignant, contribuable,…
- une personne morale : fournisseur, prestataire, direction, section, promotion,…
- un objet physique : article, véhicule, composant, ingrédient, pièce,…
- un objet contractuel ou administratif : fiche de paye, contrat, procès verbal, billet, dossier…
- un lieu : salle, local, manufacture, entrepôt, ligne de production,…
- un événement : transaction, jugement, achat, vente, acte administratif, appel téléphonique,…
- etc…
6.1.2 Stockage des données
- D’un point de vue informatique, un jeu de valeurs recueilli est appelé un enregistrement
- correspondant à l’encodage des données recueillies sur un support numérique
- Une structure de données définit les données de manière logique,
- c’est à dire l’ordre dans lequel elles doivent être lues
- et la manière dont elles doivent être interprétées par les programmes qui les utilisent.
- listes,
- listes de listes,
- dictionnaires,
- arbres,…
- Les types des valeurs étant déterminés (selon les cas de taille fixe ou variable),
- la structure de données correspond au “véhicule” qui servira à transporter et échanger les données (entre programmes, entre ordinateurs).
- Différentes structures de données sont possibles pour l’encodage et le stockage d’un jeu de valeurs, voir :
- Données non structurées
- Données vectorielles
- Tuples
- Données structurées
- Données Hiérarchisées
Tuples
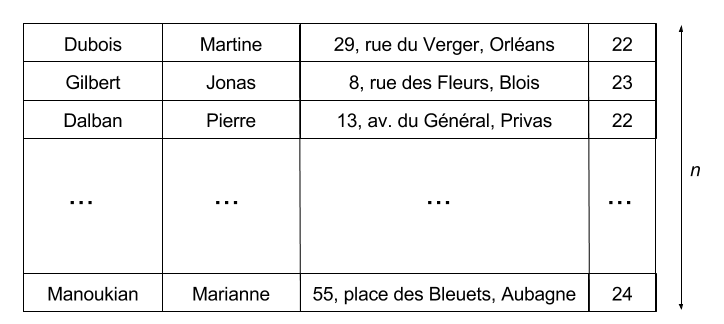
Le Tuple est la structure de données de base servant pour le recueil, le transport et le stockage des données.
- Un Tuple est une liste, finie, ordonnée et de taille fixe contenant une suite de valeurs.
- Chaque valeur peut obéir à un format différent
- On note m la taille du tuple (nombre de valeurs)
$$ t = (a_1, ..., a_m) $$ Exemple :
("Dubois", "Martine", 22, "29/10/1994", "Orléans")
<!--
=== Données brutes ===
*Textes,
*comptes rendus,
*série de notes, de valeurs sans format précis :
-> format texte en général.
<note>
Le format ''txt'' désigne des données non structurées de type “texte” regroupant différents modes d’encodage :
* ASCII (caractères sans accent),
* utf8 (caractères accentués et spéciaux),
* ...
</note>
=== Données vectorielles===
* Chaque jeu de valeurs est codé sous la forme d’un **vecteur**
* constitué de grandeurs entières ou réelles :
* toutes les valeurs sont quantitatives (numériques).
* C’est un encodage adapté aux grandeurs physiques :
* chaque champ du formulaire est codé dans un format numérique
* il est possible de représenter les données dans un espace vectoriel
<note important> Un **vecteur** est une séquence (ordonnée et finie) de valeurs quantitatives, chaque valeur obéissant au même format numérique.
</note>
<note tip>
**Exemple** :
Considérons une station météorologique enregistrant à intervalle réguliers les données de ses capteurs :
* thermomètre,
* baromètre,
* hygromètre
* et anémomètre.
Un jeu de valeurs sera constitué de //5 réels double précision// décrivant
* la température,
* la pression,
* l’humidité,
* la vitesse
* et la direction du vent.
</note>
=== Tuples===
**NB**:
* Les données sont organisées sous la forme d’une liste de valeurs qualitatives ou quantitatives.
* Le tuple est la structure de base servant pour la transmission des données (simple, facile à coder et à échanger).
-->
NB: un tuple est une séquence (ordonnée et finie) de valeurs, chaque valeur pouvant être de type qualitatif ou quantitatif, et pouvant obéir à un format numérique différent.
- les composants 1, 2, 5 et 7 sont des chaînes de caractères
- les composants 3, 4 et 6 sont des entiers
Chaque enregistrement est codé sur une ligne, chaque valeur étant séparé par un caractère séparateur (virgule, point-virgule, tabulation,…).
Exemple :
Dubois,Martine,"28, rue des Lilas, 45000 Orléans",45
Remarques :
- les données sont des chaînes de caractères
- les guillemets sont nécessaires lorsque la valeur contient le caractère séparateur (ici la virgule)
- les noms des attributs sont éventuellement indiqué sur une ligne séparée
Données indexées
- Données organisées sous la forme d’une liste d’attributs.
- Chaque attribut est défini par un nom et un format (type).
- Chaque valeur est stockée sous la forme d’un couple (attribut : valeur).
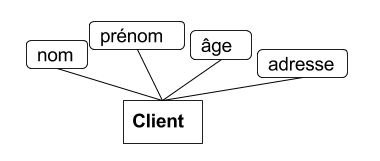
Considérons une fiche servant à décrire un étudiant. L’étudiant doit remplir les rubriques nom, prénom et âge, numero de voie, nom de la voie, code postal, ville.
Chaque rubrique correspond à un attribut, où:
- nom, prenom, voie, et ville sont des attributs de type chaîne de caractères
- age et numero et code_postal sont des attributs de type entier
La structure de données sous-jacente est le dictionnaire, où l’attribut est la clé permettant d’accéder à la valeur.
Exemple :
{"nom" : "Dubois", "prénom" : "Martine", "adresse" : "28, rue des Lilas, 45000, Orléans", "âge" : 45}
Remarques :
- reprend la syntaxe vue en Python
- données numériques ou chaînes de caractères
Données Hiérarchisées
- Organisation des données correspondant à une structure d’arbre.
- Dans le cas d’un recueil de données, correspond à la définition de rubriques et sous-rubriques.
- La rubrique adresse peut contenir les sous-rubriques numero, voie, code_postal et ville.
- Un document contient des chapitres, des sections, des sous-sections etc…
Pour les données organisées de manière hiérarchique. Des balises servent à séparer les différents attributs.
Ex :
<nom> Dubois </nom> <prénom> Martine </prénom> <adresse> <num> 28 </num> <voie> rue des Lilas </voie> <code postal> 45000 </code postal> <ville> Orléans </ville> </adresse> <âge> 45 </âge>
remarque : le format json permet également de définir des hiérarchies
{
"nom" : "Dubois",
"prénom" : "Martine",
"adresse" :
{
"numero" : 28,
"voie" : "rue des Lilas",
"code_postal" : 45000,
"ville" : "Orléans"
},
"âge" : 45
}
Tableaux de données
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
6.2 Schéma et relation
2 approches en modélisation :
- approche ensembliste (plus général)
- modèle relationnel (plus pratique)
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
Rappel:
- Un enregistrement est un jeu de valeurs organisé sous forme de tuple
- A un tuple on associe en général un schéma de données.
- Définir un schéma consiste à définir :
- une liste d'attributs (labels) associées à chacune des valeurs du tuples.
- A chaque attribut correspond :
- un intitulé
- un domaine de valeurs (type/format des données)
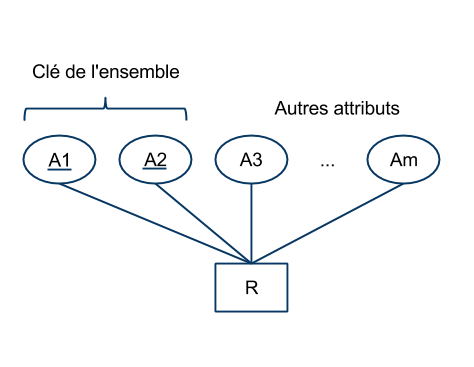
- Soit $R(A_1, ..., A_m)$ un schéma.
- On note $\text{dom}(A_i)$ le domaine associé à l'attribut $A_i$.
- On dit d'un tuple $t$ qu'il obéit au schéma $R$ si les valeurs qu'il contient correspondent aux domaines des attributs du schéma.
Soit $R = (A_1,...,A_m)$ un schéma de données
Une relation $r$ obéissant au schéma $R$ est un sous-ensemble du produit cartésien $\text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- avec :
- $\forall (i,j), a_{ij} \in \text{dom}(A_j), $
- $\forall i, t_i \in \text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- $n$ : nombre de tuples
- $m$ : nombre d'attributs par tuple
- Le schéma $R$ représente le niveau abstrait (modélisation)
- La relation $r$ représente un cas concret de réalisaton (à un schéma $R$ peuvent correspondre une infinité de réalisations possibles : $r$, $r'$, $r''$, etc. )
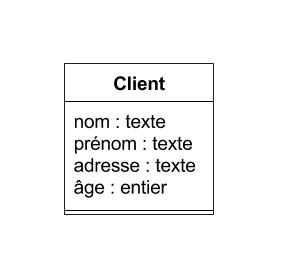
UML :
Client(nom, prénom, adresse, âge)
Étudiant(nom, prénom, adresse, INE)
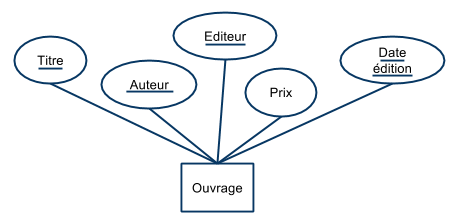
Ouvrage(titre, auteur, éditeur, prix, date_édition)
Véhicule(immatriculation, marque, modèle, couleur)
6.3 Dépendances fonctionnelles
- Au sein d'un schéma $R$,
- Il peut exister un ensemble de contraintes, noté $F$,
- portant sur les attributs (plus précisément sur les valeurs prises par les attributs).
- L'ensemble F est indépendant de R.
- On parle de contraintes d’intégrité.
- Ces contraintes s’expriment sous la forme de dépendances fonctionnelles.
- Relation binaire : une relation binaire $r$ portant sur deux domaines $\text{dom}(A)$ et $\text{dom}(B)$:
- est un sous-ensemble du produit cartésien $\text{dom}(A) \times \text{dom}(B)$.
- si $(a,b) \in r$, on note parfois $a r b$ ce qui signifie “a est en relation avec b”.
- Fonction : une fonction $f : \text{dom}(A) \rightarrow \text{dom}(B)$ est une relation binaire sur $\text{dom}(A) \times \text{dom}(B)$ telle que
- pour tout $a \in \text{dom}(A)$,
- il existe un unique $b$ tel que $(a,b) \in f$.
- On note $b=f(a)$ ,
- ce qui signifie qu'au sein de la relation $f$, $b$ est déterminé de façon unique par le choix de $a$ (autrement dit : “b dépend de a”)
- Soit $r$ une relation définie selon $R(A_1,...,A_m)$
- Soient $X$ et $Y$ deux sous-ensembles de $R$
- On dit que la relation $r$ définit une dépendance fonctionnelle de $X$ vers $Y$,
- notée $X \stackrel{r}{\rightarrow} Y$
- si les valeurs de $r$ permettent de définir une fonction de $\text{dom}(X)$ vers $\text{dom}(Y)$.
Soit la relation $r$:
| A | B | C |
|---|---|---|
| 1 | a | e |
| 2 | b | f |
| 2 | c | f |
| 3 | d | k |
| 4 | d | k |
- On a les dépendances suivantes :
- $A \rightarrow C$
- $B \rightarrow C$
- mais pas : $A \rightarrow B$, $B \rightarrow A$, ni $C \rightarrow A$
- On a aussi :
- $A,B \rightarrow C$
- mais pas : $B,C \rightarrow A$, ni $A,C \rightarrow B$, etc.
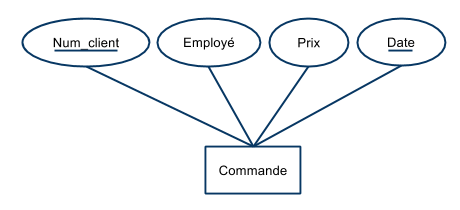
- Soit le schéma :
- Commande (num_client, quantité, prix, date, num_article)
- et l’ensemble de contraintes
$$ \begin{array}{rl}F &= \{\\ & \text{num_client, date} \rightarrow \text{num_article, quantité, prix} \\ & \text{num_article, quantité} \rightarrow \text{prix} \\ &\} \end{array} $$
- La première contrainte indique qu'il ne peut y avoir deux factures émises pour un même client à une date donnée.
- La seconde contrainte indique que le prix payé dépend de l’article et de la quantité commandée.
- Soit le schéma :
- Ouvrage (titre, auteur, éditeur, prix, date_edition)
- et la contrainte :
- {titre, auteur, éditeur → prix, date_édition}
La contrainte signifie :
- “pour une oeuvre chez un certain éditeur, une seule édition est possible (pas de réédition à une date ultérieure)”
- “politique du prix unique”
- Réservation(code_appareil, date, heure, salle)
Exprimer la dépendance fonctionnelle :
- « Un appareil ne peut pas être utilisé dans deux locaux différents au même moment »
- Il importe donc de bien réfléchir, au moment de l'étape de conception,
- du réalisme et du caractère limitant de certaines dépendances fonctionnelles,
- et du caractère éventuellement limitant du choix des attributs.
- Ainsi, le schéma décrivant les commandes (exemple 2)
- ne permet pas de commander des articles de nature différente au sein d'une même commande
- (un client, pour commander deux râteaux et une truelle, doit donc effectuer deux commandes, qui plus est à des dates différentes!).
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Définir des dépendances fonctionnelles sur cet ensemble d'attributs
6.4 Clé d'une relation
6.4.1 Définitions
- Soit un schéma $R(A_1, ..., A_m)$.
- Une clé $K$ :
- est un ensemble minimal d'attributs inclus dans R,
- tel que toute relation $r$ de schéma $R$ définit une dépendance fonctionnelle de $dom(K)$ dans $dom(R)$,
- cette dépendance est notée $K \rightarrow R$.
- Remarques :
- Si un schéma $R$ possède une clé $K$, alors tous les éléments d’une relation $r$ de schéma $R$ sont discernables : la valeur de la clé permet d’identifier de façon unique chaque élément de l’ensemble.
- Au sein d'un schéma, il est souvent possible de définir plusieurs clés à partir des attributs. Le concepteur du modèle choisit une clé parmi les clés possibles. Cette clé est appelée clé primaire.
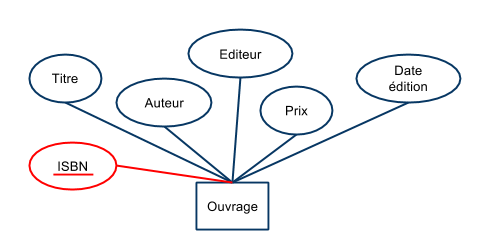
- Graphiquement, les attributs constituant la clé sont soulignés:
- Pour certains schémas,
- il est courant de définir comme clé un entier identifiant de façon unique chaque élément de l'ensemble (appelé identifiant ou “Id”).
- La clé est alors constituée de cet attribut unique.
Représentation UML :

6.4.2 Axiomes d'Amstrong
Soit $K$ une clé candidate. On démontre que $K \rightarrow R$ à l'aide des axiomes d'Amstrong à partir d'un ensemble de DF connues:
- Réflexivité : $$Y \subseteq X \Rightarrow X \rightarrow Y$$
- Augmentation : $$X \rightarrow Y \Rightarrow X,Z \rightarrow Y,Z$$
- Transitivité : $$X \rightarrow Y \text{ et } Y \rightarrow Z \Rightarrow X \rightarrow Z$$
- Pseudo-transitivité : $$X \rightarrow Y \text{ et } Y,W \rightarrow Z \Rightarrow X,W \rightarrow Z$$
- Union : $$X \rightarrow Y \text{ et } X \rightarrow Z \Rightarrow X \rightarrow Y,Z$$
- Décomposition : $$X \rightarrow Y, Z \Rightarrow X \rightarrow Y \text{ et } X -> Z$$
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Montrer que l'ensemble {num_train, num_voiture, num_place, date, gare_départ} est une clé primaire du schéma?
6.4 Normalisation d'un schéma
Tables mal construites
$$\textbf{Fournisseur}(\underline{\text{nom_f, composant}}, \text{adresse_f, prix})$$
- Problèmes :
- Redondance : l’adresse des fournisseurs est répétée plusieurs fois
- Inconsistance : mauvaise mise à jour ⇒ adresses différentes pour un même fournisseur.
- Problème Insertion : on ne peut pas insérer dans la table un fournisseur qui ne fournit rien
- Problème suppression : si un fournisseur ne fournit plus rien, on perd son adresse
- Solution?
- Couper la table en 2?
–> Impossible de retrouver les prix pratiqués par les différents fournisseurs.
- Nouveau Schéma :
–> Il est possible de reconstruire la table initiale en effectuant une jointure entre ces 2 tables sur l’attribut nom_f.
- Enseignement (id_enseignant, nom_enseignant, matière, id_élève, nom_élève)
- Arrêt (num_train, horaire, nom_gare, ville)
- Facture (id_client, date, article, montant)
6.5 Formes Normales
Les Formes normales
- Restreignent les dépendances admises dans un schéma relationnel
- Permettent d’éviter la duplication de l’information au sein des relations
- Définissent une méthode
- de décomposition d’un schéma relationnel redondant
- en plusieurs schémas liés entre eux:
6.5.1 2ème forme normale (2FN)
- Soit $R$ un schéma relationnel
- Soit $X$ un ensemble d’attributs ⊆ $R$
- Soit $A$ un attribut de $R$
- Il existe une DFE entre $X$ et $A$ ssi :
- $X \rightarrow A$
- Il n’existe aucun sous-ensemble $Y$ ⊆ $X$ tel que $Y \rightarrow A$
- Un schéma $R$ est en 2FN :
- ssi la clé primaire de $R$ est en DFE avec tous les autres attributs.
- Donc : il n’y a pas d’attributs qui ne dépendent que d’une partie de la clé.
6.5.2 Normalisation 2FN
- Lorsqu’un schéma relationnel n’est pas en deuxième forme normale, il doit être normalisé:
- Pour obtenir un schéma 2FN:
- on “découpe” la table selon les DFE trouvées entre les attributs de la clé et ceux qui ne sont pas dans la clé.
- La normalisation consiste:
- à créer une nouvelle table pour chaque DFE ainsi trouvée.
- Soit :
$$\mathbf{R} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,\color{red}{B_j},...,B_m)$$
- avec :
$$\color{red}{A_i} \stackrel{DFE}{\rightarrow} \color{red}{B_j}$$ $$A_1,...,\color{red}{A_i},...,A_n \stackrel{DFE}{\rightarrow} B_1,...,B_{j-1},B_{j+1}...,B_m$$
- Alors le schéma de table doit être modifié comme suit :
$$\mathbf{R_1} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,B_{j-1},B_{j+1}...,B_m)$$ $$\mathbf{R_2} (\underline{\color{red}{A_i}},\color{red}{B_j})$$
Même si aucun attribut ne dépend plus de la clé primaire initiale, il est important de la conserver dans une table spécifique (elle sert à “lier” les valeurs dispersées dans les différentes tables).
- Avant:
$$\textbf{Fournisseur}(\underline{\text{nom_f,composant}}, \text{adresse_f, prix})$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$ $$\text{nom_f, composant} \rightarrow \text{prix}$$
- Après:
$$\textbf{Catalogue}(\underline{\text{nom_f,composant}}, \text{prix})$$ $$\textbf{Fournisseur}(\underline{\text{nom_f}}, \text{adresse_f})$$
- Les tables ont un attribut commun : nom_f (clé primaire de la table Fournisseur).
- La clé primaire de la table des Fournisseurs est dupliquée dans la table des prix (appelée ici Catalogue).
- On dit que nom_f est une clé étrangère de la table des prix (l’attribut fait référence à la clé primaire d’une autre table, en l’occurrence la table des fournisseurs - voir 3.1.1).
6.5.3 3ème forme normale (3FN)
La dépendance fonctionnelle entre 2 attributs $A_i$ et $A_j$ est directe s’il n’existe pas de $A_k$ tel que : $$A_i \rightarrow A_k \rightarrow A_j$$
Un schéma est 3FN :
- S’il est 2FN
- Si tous les attributs sont en DFD avec la clé.
$$\textbf{Commande} (\underline{\text{num_commande}}, \text{nom_f, adresse_f, composant, quantité})$$ $$\text{num_commande} \rightarrow \text{nom_f, composant, quantité}$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$
Le schéma n’est pas 3FN!! (dépendance transitive entre num_commande et adresse)
6.5.4 Normalisation 3FN
* Lorsqu’un schéma relationnel n’est pas en troisième forme normale, il doit être normalisé:
- On crée une table pour chaque DFD trouvée au sein des attributs n'appartenant pas à la clé.
Soit : $$R (\underline{A_1,...,A_m},B_1, ..., \color{red}{B_i},...,\color{red}{B_j},...,B_n)$$ avec : $$A_1, ..., A_m \stackrel{DFD}{\rightarrow} B_1, ...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n$$ $$\color{red}{B_i} \stackrel{DFD}{\rightarrow} \color{red}{B_j}$$ Alors : $$R_1 (\underline{A_1,...,A_m},B_1,...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n)$$ $$R_2 (\underline{\color{red}{B_i}},\color{red}{B_j})$$
Comme précédemment, il est important de conserver la clé primaire de la table initiale si elle permet d'associer les valeurs dispersées dans les tables.
Avant :
- Commande (num_commande, nom_f, adresse_f, composant, quantité)
- avec :
- num_commande → nom_f, composant, quantité
- nom_f → adresse_f
Après :
- Commande (num_commande, nom_f, composant, quantité)
- Client (nom_f, adresse_f)
L’attribut nom_f est maintenant clé primaire de la table Client et clé étrangère de la table Commande.
6.6 Modèle ensembliste
Une base de donnée est constituée de plusieurs ensembles d'objets et d'opérateurs participant au bon fonctionnement d'un système:
Exemple 1 :
- Ensembles d'employés
- Ensembles de commandes
- Ensembles d'articles
- Ensembles de clients
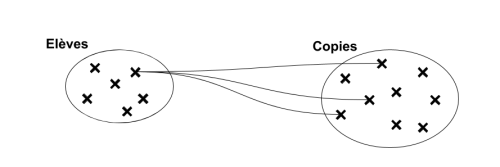
Exemple 2 :
- Ensembles d'étudiants
- Ensembles de séances
- Ensembles de cours
- Ensembles de copies
On parle plus généralement d'ensembles d'entités.
Le modèle entité/associations est une méthode de description des relations entre ensembles d’entités. Il s’appuie sur le prédicat selon lequel tous les éléments des ensembles d’entités sont discernables.
Le modèle entités/associations repose sur un langage graphique de description des données, indépendant du support et de la mise en œuvre informatique.
Généralités
Une entité $x$
- est une représentation d'un objet du monde réel,
- appartenant au système/à l'organisation modélisée.
- Une entité est décrite par une ou plusieurs valeurs caractéristiques, appelées attributs.
Les informations conservées au sujet des entités d'un ensemble sont les attributs.
- Chaque attribut :
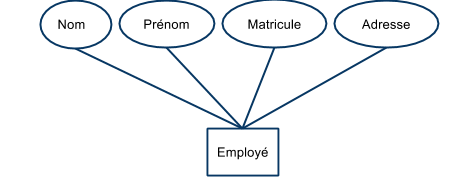
- a un nom unique dans le contexte de cet ensemble d'entités : $A$, $B$, $C$, $A_1$, $A_2$, …, $A_m$, …
- Exemples de noms concrets : couleur, nom, horaire, salaire.
- prend ses valeurs dans un domaine bien spécifié,
- également appelé le type de l'attribut.
- Le domaine d'un attribut est noté $\text{dom}(Aj)= Dj$.
- Exemples :
- $\text{dom}(couleur)={rouge, vert, bleu, jaune}$,
- $\text{dom}(nom) = $ensemble des chaînes de caractères,
- $\text{dom}(salaire) =$ entiers naturels
- etc…
- Un attribut $A_j$ est une fonction à valeur sur $D_j$ :
$$A_j : E \rightarrow D_j$$ $$x \mapsto A_j(x)$$
- Un attribut peut être :
- simple ou composé.
- Exemple : une adresse peut être décrite par une simple chaîne de caractères, ou peut être décomposée en rue , no, boîte, ville, code postal, pays.
- obligatoire ou facultatif ($D_j$ peut ou non contenir la valeur ø ).
- atomique ou non (Un attribut peut posséder 0, 1 voire plusieurs valeurs…)
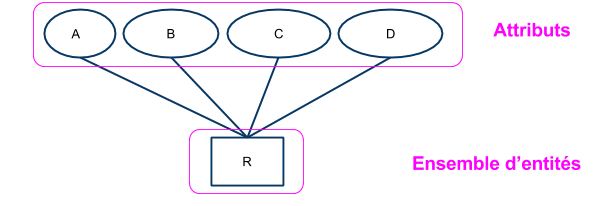
Un ensemble d'entités est un ensemble fini d'éléments : $$E = \{x_1,…,x_n\}$$ Il regroupe (ou associe) plusieurs entités ayant des caractéristiques communes (descriptibles à l'aide du même ensemble d'attributs).
- les employés d'une firme,
- les cours de Centrale Méditerranée,
- une collection de disques,
- etc…
- Les éléments d’un ensemble d’entités sont partiellement discernables à travers les valeurs de leurs attributs :
- les attributs $(A_1,...,A_m)$ servent à décrire les éléments de l’ensemble.
- Le schéma $R$ de l’ensemble $E$ est une application de l'ensemble d'entités vers l'ensemble des tuples de schéma $R$
- Soit :
$$ R : \mathcal{X} \rightarrow D_1 \times ... \times D_m$$ $$ x_i \mapsto (A_1(x_i),…, A_m(x_i))$$
Définitions
Modéliser une base de données, c'est :
- Identifier les différents ensembles en interaction
- Identifier les liens de dépendance entre les différents ensembles
Association
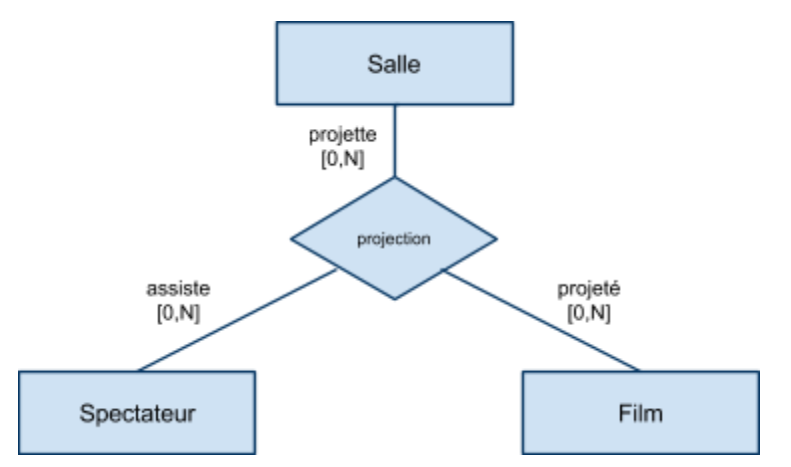
Définition : Une association entre les ensembles $E_1$, …, $E_k$ est un sous-ensemble du produit $E_1 \times ... \times E_k$.
Il s'agit donc d'un ensemble de k-uplets $\{..., (x_1,…,x_k), …\}$ t.q. $x_1 \in E_1,…, x_k \in E_k$.
où $k$ est le degré de l'association :
- k=2 : association binaire
- k=3 : association ternaire
- etc…
Rôles des associations
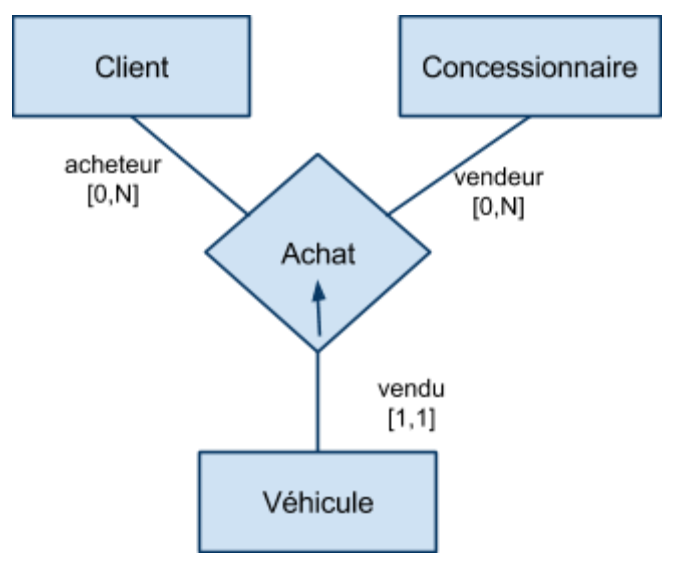
- Attribution : propriété, réservation, participation, supervision, auteur, rôle, pilote, …
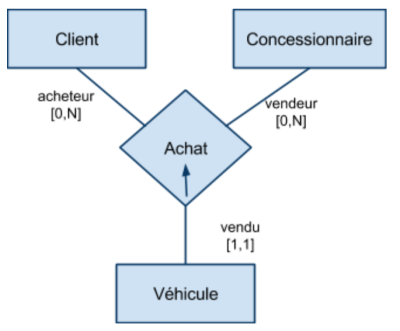
- Événements : achat, vente, séance, épreuve, appel, consultation, réunion, transaction, transport …
- Aggrégation/Composition : tout/parties, contenant/contenu, supérieur/subordonné, pays/région, …
- Relations entre membres : parenté, collaboration, cercle d'amis, …
- …
Contraintes de cardinalité
On donne en général un intervalle $[b_\text{inf},b_\text{sup}]$ qui définit le nombre d'apparitions autorisées pour chaque rôle de l'association
Représentation graphique
Types d'associations
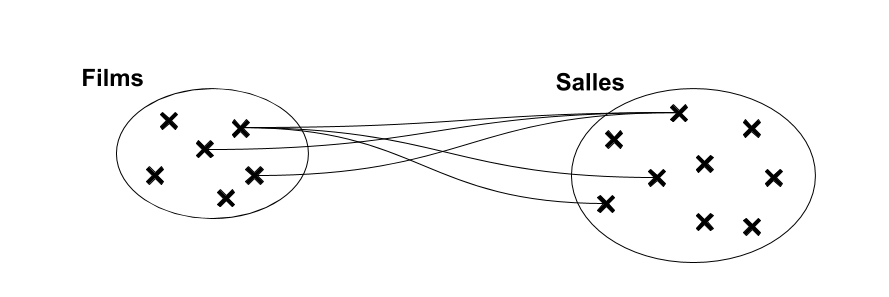
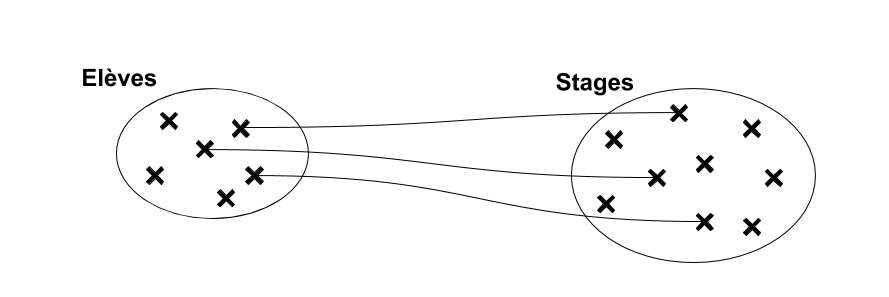
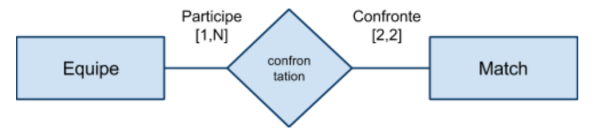
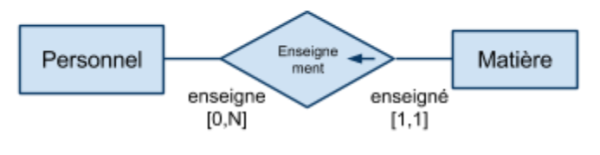
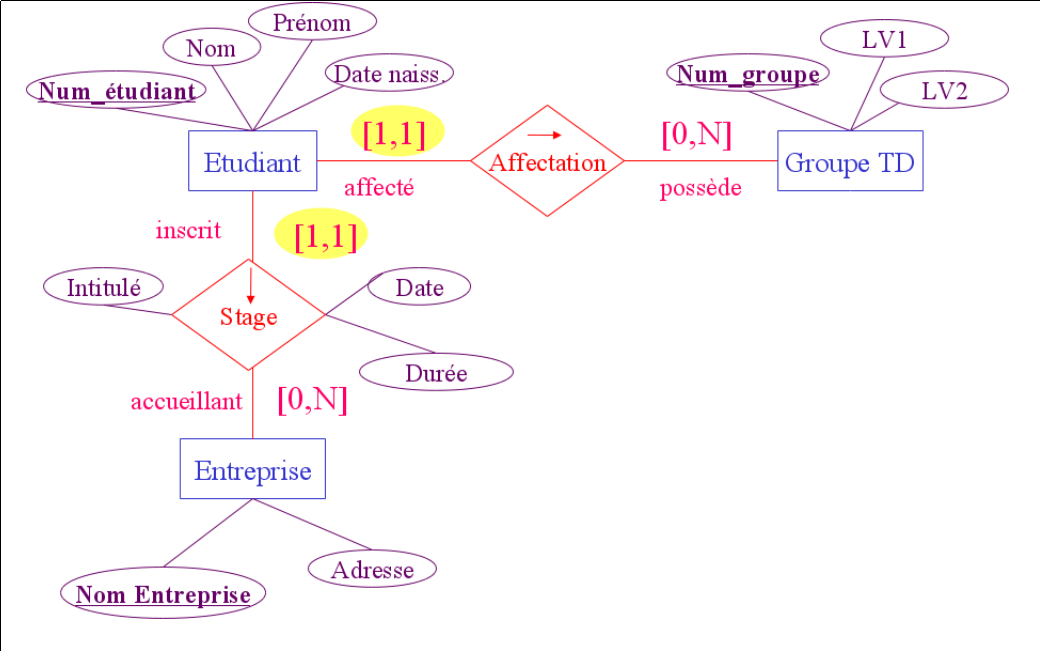
Associations de 1 à plusieurs (fonctionnelle)
Relation non symétrique entre les deux ensembles : […,1] d'un côté, […,N] de l'autre. Relation de type contenant/contenu, propriétaire/objet possédé, occupant/occupé, actif/passif etc… Il s'agit du type d'association le plus "courant".
“à gauche” → “à droite”
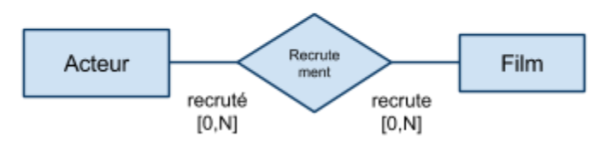
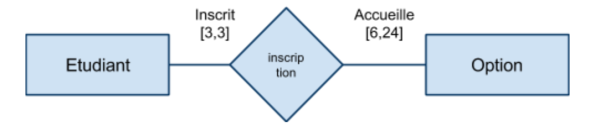
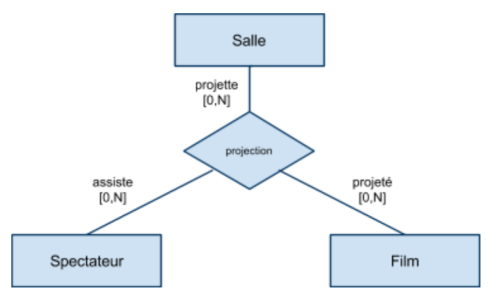
Associations de plusieurs à plusieurs (croisée)
Dans une association “croisée”, les tous les lien de l’association sont de cardinalité multiple […,N]
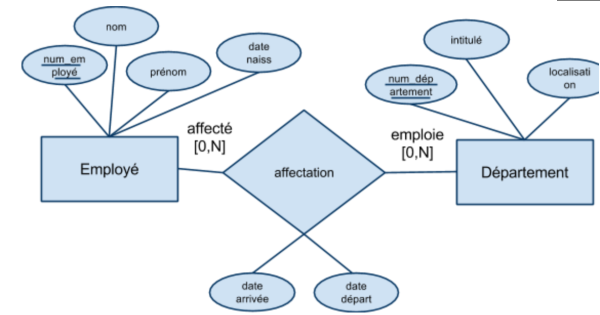
Modèles Entité Associations valués
- les attributs des ensembles d'entités sont des mesures:
- Soit $A$ un attribut de l'ensemble d'entités $\mathcal{E}$
$$ A : \mathcal{E} \rightarrow \text{dom}(A) $$
- les attributs des associations sont des opérateurs :
- Soit $B$ un attribut de l'association sur $\mathcal{E} \times \mathcal{F}$
$$ B : \mathcal{E}\times \mathcal{F}\rightarrow \text{dom}(B) $$
Mesures
- Les mesures sont les données saisies sur les éléments d'un ensemble. Chaque mesure est associée à un attribut.
- Le schéma de l'ensemble est l'ensemble des attributs servant à caractériser ses éléments
- Les éléments de l'ensemble sont discernables ssi il existe un jeu de mesures différent pour chaque élément de l'ensemble
- Une clé est un ensemble d'attributs minimal (permettant de distinguer les objets) appartenant au schéma
Ensembles discernables / non discernables
Opérateurs
- On s’intéresse ici aux associations qui représentent une “opération” (inscription, achat, embauche, affectation…).
- Lors d’une mise à jour de la base, certains événements tels que l’emprunt ou le retour d’un ouvrage, l’affectation d’un employé à un poste, ou la liste des anciens clients disparaissent.
- Il est possible de garder une trace des événements passés en mettant un (ou plusieurs) attributs sur une association.
- Ainsi, certaines associations peuvent être "datées", c'est à dire
- avoir lieu à une date
- ou prendre place sur une durée précise (prêt,accès temporaire, statut temporaire…)
- On peut ainsi mémoriser :
- "Monsieur Dupont a été employé au département logistique de tant à tant."…
- "L'étudiant X a été élève Centrale Méditerranée de telle année à telle année"…
- Chaque coureur est décrit par ses nom, prénom, nationalité et numéro de maillot.
- Chaque coureur appartient à une équipe qui possède un numéro, un sponsor associé.
- Chaque coureur participe à une ou plusieurs étapes. Une étape se caractérise par son numéro, son type (contre la montre/étape simple), ses points de départ et d'arrivée, sa date.
- A chaque étape est associée un classement d'arrivée pour chaque coureur, avec la durée totale de course.
6.6.2 Traduction vers le modèle relationnel
Il est possible de traduire un modèle entité/association vers un modèle relationnel (en perdant quelques propriétés).
- Conception de la base sous forme d'un modèle entité/association.
- Traduction sous la forme d'un modèle relationnel.
- Normalisation (voir Normalisation d'un schéma)
- Mise en œuvre informatique.
Un petit nombre de règles permettent de traduire un modèle entité/association vers un modèle relationnel.
- Selon ces règles, à la fois les ensembles d'entités et les associations sont transformés en schémas relationnels.
- Les liaisons et dépendances entre schémas de relation sont assurés par la définition des clés étrangères (attributs communs à plusieurs tables).
Schéma de base et clé étrangère
- Un schéma (ou modèle) de bases de données est un ensemble fini de schémas de relation.
- Une base de données est un ensemble fini de relations.
- Les liens et associations entre relations entre s’expriment sous la forme de clés étrangères
- Au sein d'un schéma relationnel $R$, Une clé étrangère est un attribut (ou un groupe d'attributs) qui constitue la clé primaire d'un schéma $S$ distinct de $R$.
- La présence d'une clé étrangère au sein d'une relation $r$ de schéma $R$ introduit une contrainte d'intégrité sur les données :
- la valeur des attributs de la clé étrangère d'un tuple de $r$ doit être trouvée dans la table s correspondante.
- On indique la présence d'une clé étrangère à l'aide de pointillés : {…, Clé étrangère, …}
Exemple
- Clients ( nom_client, adresse_client, solde)
- Commandes ( num_Commande, nom client, composant, quantité)
- Fournisseurs ( nom_fournisseur, adresse_fournisseur)
- Catalogue ( nom_fournisseur, composant, prix )
Traduction des associations de plusieurs à plusieurs
Une association croisée ne contient que des contraintes de cardinalité de type [..,N]. Soit $R$ une telle association et $E_1$, …, $E_k$ les ensembles participant à l'association.
- Chaque ensemble $E_i$ est traduit par un schéma relationnel (contenant les mêmes attributs)
- L'association $R$ est traduite sous la forme d'un schéma relationnel contenant:
- les clés primaires des ensembles participant à l’association
- (éventuellement) les attributs propres à l'association,
Traduction des associations de un à plusieurs
Soit une association fonctionnelle $R$. On suppose qu'il existe au moins un ensemble $A$ de cardinalité unique [1,1] participant l’association.
- Chaque ensemble participant est traduit sous forme de schéma relationnel
- L'association $R$ est traduite sous forme de clé étrangère : l'ensemble $A$ reçoit la clé primaire du (ou des) ensemble(s) dont la participation est multiple.
Exemple complet
- Clients ( nom_client, adresse_client, solde)
- Commandes ( num_Commande, nom client, composant, quantité, montant)
- Fournisseurs ( nom_fournisseur, adresse_fournisseur)
- Catalogue ( nom_fournisseur, composant, prix )
Clients :
| nom_client | adresse_client | solde |
|---|---|---|
| Durand | 7, rue des Lilas | 335,00 |
| Dubois | 44, av. du Maréchal Louis | 744,00 |
| Duval | 5, place du marché | 33,00 |
Commandes :
| num_Commande | nom client | composant | quantité |
|---|---|---|---|
| 6674 | Dubois | micro controller | 55 |
| 6637 | Dubois | radio tuner | 2 |
| 6524 | Durand | transistor | 4 |
| 6443 | Duval | micro controller | 7 |
Fournisseurs :
| nom_fournisseur | adresse_fournisseur |
|---|---|
| Sage | 33, College street, London |
| MoxCom | 77 Ashley square,Mumbay |
Catalogue :
| nom_fournisseur | composant | prix |
|---|---|---|
| Sage | transistor | 4,4 |
| MoxCom | micro controller | 3,7 |
| MoxCom | radio tuner | 7,0 |
6.6.3 Gestionnaire de Bases de données
- Une base de données est un ensemble de tables (parfois appelées relations).
- Une table est un ensemble de tuples (parfois appelés enregistrements).
- Un tuple est un ensemble de valeurs (parfois appelés « champs » ou attributs).
Un SGBD (Système de Gestion de Bases de Données) est un programme qui gère une (ou des) base(s) de données. Il s’agit d’un programme optimisé afin d’accélérer l’accès et rationaliser le traitement d’un grand ensemble d’enregistrements stockés sur un support informatique.
Le fonctionnement d'un tel programme repose sur :
- des méthodes de conception ensemblistes fondées sur le modèle relationnel (description des ensembles d’enregistrements et des relations entre ces ensembles)
- un langage de requête permettant de consulter et mettre à jour les données stockées dans la base
- des algorithmes de stockage et de classement efficace (afin d’accélérer les temps de recherche)
Il existe enfin un administrateur de bases de données. Celui-ci doit :
- installer la base de données,
- gérer sa sauvegarde régulière,
- garantir sa sécurité et
- gérer les droits des utilisateurs de la base.
SQL (Structured Query Language)
SQL :
- est un langage de création et d'interrogation de bases de données,
- supporté par la plupart des systèmes de gestion de bases de données relationnelles du marché.
- un langage de définition de données (LDD, ou en anglais DDL, Data definition language), qui permet la description de la structure de la base (tables, vues, index, attributs, …).
- un langage de manipulation de données (LMD, ou en anglais DML, Data manipulation language), c'est la partie la plus courante et la plus visible de SQL, qui permet la manipulation des tables et des vues.
- et un langage de contrôle de données (LCD, ou en anglais DCL, Data control language), qui contient les primitives de gestion des transactions et des privilèges d'accès aux données.
CREATE TABLE Commande ( num_commande INTEGER NOT NULL, nom_client VARCHAR(30), nom_fournisseur VARCHAR(30), composant VARCHAR(30), quantité INTEGER, montant DECIMAL(12,2) NOT NULL, PRIMARY KEY (num_commande), FOREIGN KEY (nom_client) REFERENCES Client, FOREIGN KEY (nom_fournisseur, composant) REFERENCES Catalogue);
- Création :
INSERT INTO Client VALUES ("Durand", "7, rue des Lilas" , 335.00);
- Mise à jour
UPDATE Client SET adresse = "9, rue des Lilas" WHERE nom_client="Durand";
- Suppression
DELETE FROM Client WHERE nom_client="Durand";
Voir : sql.pdf
6.7 - Recherche d'information
6.7.1 Interrogation des Bases de Données
Interroger une base de données , c’est sélectionner certaines données parmi l'ensemble des données proposés.
En informatique, une requête (en anglais query) est une demande de consultation ou d'édition, effectuée par un programme client à l’attention d’un programme serveur.
- Le programme client représente l’utilisateur, il s’agit du programme qui enregistre la demande de l’utilisateur, la transmet au serveur, puis met en forme visuellement la réponse du serveur.
- Les données sont centralisées au niveau du serveur, chargé de la gestion, de la manipulation et du stockage des données.Il traite la requête, consulte les données et transmet le résultat au client.
Consultation des données
La requête peut être une simple référence vers un fichier, ou être l’expression d’une recherche plus spécifique (consultation de certaines fiches d’un fichier, croisement d’information (entre plusieurs fichiers), etc…). Dans ce cas, il est nécessaire d’utiliser un langage de requête (le plus souvent SQL).
On distingue quatre grands types de requêtes (approche “CRUD”):
- Création (Create) : ajout de nouvelles données dans la base
- Lecture/recherche (Read) : consulation du contenu de la base
- Mise à jour (Update) : changement du contenu existant
- Suppression (Delete) : suppression des données obsolètes
Lors d’une consultation de type lecture/recherche, il y a souvent plusieurs réponses qui correspondent à la demande. Le résultat d’une requête prend donc la forme d’un ensemble de réponses. Ces réponses sont éventuellement classées, selon la valeur d’un certain identifiant, ou selon le degré de pertinence.
- requêtes http : demande de consultation d’une page web ( = référence vers un fichier)
- moteur de recherche : recherche de pages contenant les mots-clés spécifiés
- bases de données : utilisation d’un langage de requête :
SELECT * FROM Eleves WHERE NOM = 'Dugenou'
Exemples :
- croisement de facteurs de recherche :
- Donner la liste des pays exportateurs de pétrole
- Liste des musiciens jouant à la fois du piano et du violon
- Liste des artistes français disque d'or en 1977
- Liste des suspects châtain taille moyenne présents à Poitiers la nuit du 12 au 13 février
- Analyse des données
- faire ressortir des corrélations (exemple : type d'habitat/intentions de vote),
- pour des enquêtes de consommation, du marketing ciblé …
- Information personnalisée :
- ne retenir que les informations utiles à un instant et pour une personne donnée.
- Emploi du temps de l'élève X pour la semaine Y.
- Factures impayées du client Z
- il y a souvent plusieurs réponses qui correspondent à la demande.
- Le résultat d’une requête prend donc la forme d’un ensemble de réponses.
- Ces réponses sont éventuellement classées,
- selon la valeur d’un certain identifiant,
- ou selon le degré de pertinence.
- propose un certain nombre d’opérations ensemblistes :
- Intersection,
- Union,
- Projection,
- Différence,
- …
- qui, à partir d'un ensemble de relations, permettent de construire de nouvelles relations.
- La relation nouvellement construite contient le résultat de la requête
6.7.2 Opérateurs mono-table
Extraction d'information à partir d'une table unique :
- projection $\pi$ = extraction de colonnes
- sélection $\sigma$ = extraction de lignes
Projection : π
- Soit $r$ une relation de schéma $R$.
- Soit $S$ un ensemble d'attributs, avec $S$ ⊆ $R$
La projection $\pi_S(r)$ est une nouvelle relation de schéma $S$ obtenue à partir des éléments de $r$ restreints au schéma $S$ $$\pi_S(r) = \{t(S)|t \in r\}$$
(avec $t(S)$ la restriction de $t$ au schéma $S$)
| nom_fournisseur | adresse_fournisseur | composant | prix |
|---|---|---|---|
| Sage | 33, College street, London | transistor | 4,4 |
| MoxCom | 77 Ashley square,Mumbay | micro controller | 3,7 |
| MoxCom | 77 Ashley square,Mumbay | radio tuner | 7,0 |
Requete : Donner la liste des fournisseurs (avec leur adresse): $$u = \pi_\text{nom_fournisseur, adresse_fournisseur} (\text{Catalogue})$$
$\rightarrow$ u :
| nom_fournisseur | adresse_fournisseur |
|---|---|
| Sage | 33, College street, London |
| MoxCom | 77 Ashley square,Mumbay |
Sélection : σ
- On considère le schéma $R (A_1, …, A_n)$
- Une condition $F$ sur $R$ :
- est un ensemble de contraintes sur les valeurs des attributs $A_1$, …, $A_n$
- construites à l'aide d'opérateurs booléens classiques :
- ∧(et),
- ∨(ou),
- ¬(non),
- =, ≠, >,<, ≥ ,≤, …
- et de valeurs numériques ou de texte.
- Soit $r$ une relation de schéma $R$
- Soit $F$ une condition sur $R$
La sélection $σ_F(r)$ est une nouvelle relation de schéma $R$ , constituée de l'ensemble des enregistrements de $r$ qui satisfont la condition $F$.
$$σ_F(r) = \{ t ∈ r | F( t ) \text{est vrai} \}$$
Requête : Donner la liste des fournisseurs qui vendent des micro-controleurs
$$u = Π_\text{nom_fournisseur}( σ_\text{Composant = micro controller} ( \text{Fournisseur} ))$$ u :
| nom_f |
|---|
| Moxcom |
Pays :
| nom_pays | superficie | population | PIB/hab |
|---|---|---|---|
| Algérie | 2.300.000 | 31.300.000 | 1630$ |
| Niger | 1.200.000 | 11.400.000 | 890$ |
| Arabie Saoudite | 2.150.000 | 24.300.000 | 8110$ |
Requête : Donner la liste des pays dont le PIB/hab est > 1000$ $$u = Π_\text{nom_pays}( σ_\text{PIB/hab > 1000 } ( \text{Pays} ))$$
u :
| nom_pays |
|---|
| Algérie |
| Arabie Saoudite |
Structure d'une requête SQL
SELECT A1,A2, …, An // liste d’attributs FROM R // nom de la TABLE WHERE F // condition sur les attributs
cette requête est semblable à :
- une sélection algébrique $σ_F$
- suivie par une projection algébrique $Π_{A1, …, An}$
soit : $$Π_{A1, …, An}( σ_F ( R ))$$
Exemples :
- Qui fournit des transistors ?
SELECT nom_fournisseur FROM Fournisseur WHERE composant = ’transistor’;
- Liste de toutes les commandes de transistors :
SELECT * FROM Commandes WHERE composant = ’transistor’
- Qui fournit des micro-controleurs à moins de 5$?
SELECT nom_fournisseur FROM Catalogue WHERE composant = ’micro controller’ AND prix < 5
Aspects algorithmiques
Algo de sélection :
pour tout tuple e de r:
si e obéit à la condition F:
ajouter e à la réponse
complexité : O(n)
- On parle de recherche ciblée lorsque le nombre d’éléments obéissant à la condition F est a priori très faible :
- exemple : on cherche le salaire de Mr “Dupont”.
- On parle de recherche extensive lorsque l’ensemble de valeurs obéissant à la condition F est a priori élevé.
- exemple : les employés dont le salaire est < 2000 euros
Remarque : dans le cas d'une recherche ciblée, la présence d'un index sur le critère de recherche permet d'accélérer la sélection :
pour toute a ∈ F: i ← Index(a) ajouter r[i] à la réponse
6.7.3 Opérateurs multi-tables
Principe : recoupement d'informations présentes dans plusieurs tables :
- Croisement des critères de sélection : Jointure
- Recherche ciblée : Division
La jointure : ⋈
- Soient les relations r et s de schémas R et S.
- On note R ⋂ S la liste des attributs communs aux deux schémas et R ⋃ S la liste des attributs appartenant à R ou à S.
- soit t ∈ r et q ∈ s tels que t(R ⋂ S) = q(R ⋂ S)
On note t ⋃ q le tuple formé des valeurs de t et de q étendues au schéma R ⋃ S
- Soient r et s (de schémas R et S), avec R ⋂ S = Ø
Le produit cartésien r × s est une nouvelle table de schéma R ⋃ S combinant les tuples de r et de s de toutes les façons possibles : $$r × s = \{t \cup q : t \in r, q \in s\}$$
- La jointure est une opération qui consiste à effectuer un produit cartésien des tuples de deux relations pour lesquelles certaines valeurs correspondent.
- Le résultat de l'opération est une nouvelle relation.
- Soient r et s (de schémas R et S), avec R ⋂ S ≠ Ø
- La jointure r ⋈ s est une nouvelle table de schéma R ⋃ S combinant les tuples de r et de s ayant des valeurs communes pour les attributs communs.
$$r ⋈ s = \{t \cup q : t∈ r, q∈ s, t(R \cap S) = q(R \cap S)\}$$
Matière_première :
| nom_matière | unité | prix |
|---|---|---|
| pétrole | baril | 45$ |
| gaz | GJ | 3$ |
| uranium | lb | 12$ |
Exportations :
| nom_pays | nom_matière | quantité |
|---|---|---|
| Algérie | pétrole | 180.000 |
| Algérie | gaz | 20.000 |
| Niger | uranium | 30.000 |
| Arabie Saoudite | pétrole | 2.000.000 |
| Arabie Saoudite | gaz | 750.000 |
Matière_première ⋈ Exportations :
| nom_pays | nom_matière | quantité | unité | prix |
|---|---|---|---|---|
| Algérie | pétrole | 180.000 | baril | 45$ |
| Algérie | gaz | 20.000 | GJ | 3$ |
| Niger | uranium | 30.000 | lb | 12$ |
| Arabie Saoudite | pétrole | 2.000.000 | baril | 45$ |
| Arabie Saoudite | gaz | 750.000 | GJ | 3$ |
Exemples de requêtes
- “Donner la liste des PIB/hab des pays exportateurs de pétrole” :
$$Π_\text{PIB/hab}( σ_\text{nom_matière = pétrole} ( \text{Pays} ⋈ \text{Exportations} ))$$
- Clients ( nom_client, adresse_client, solde)
- Commandes ( num_Commande, nom client, nom fournisseur, composant, quantité, montant)
- Fournisseurs ( nom_fournisseur, adresse_fournisseur)
- Catalogue ( nom_fournisseur, composant, prix )
- “Donner le nom et l'adresse des clients qui ont commandé des micro controleurs” :
$$Π_\text{nom_client,adresse_client}( σ_\text{composant = 'micro-controller'} ( \text{Client} ⋈ \text{Commandes} ))$$
Requêtes multi-tables en SQL
SELECT A1,A2, …, An // liste d’attributs FROM R1, …, Rm // liste de TABLES WHERE F1 AND … AND Fl // liste de conditions sur les attributs // (en particulier conditions sur les attributs // sur lesquel s’effectue la jointure)
Pour exprimer la jointure sur l’attribut 'Aj' commun aux tables 'R1' et 'R2', on écrira : 'R1.Aj = R2.Aj'
Exemples :
- Approche prédicative :
SELECT PIB_par_hab FROM Pays NATURAL JOIN Exportations WHERE nom_matiere = 'petrole'
SELECT PIB_par_hab FROM Pays, Exportations WHERE nom_matiere = 'petrole' AND Pays.nom_pays = Exportations.nom_pays
- Approche ensembliste :
SELECT PIB_par_hab FROM Pays WHERE nom_pays IN ( SELECT nom_pays FROM Exportations WHERE nom_matiere = 'petrole' )
Aspects algorithmiques et optimisation
Lors d’une opération de jointure, on distingue en général la “table de gauche” de la “table de droite”.
- La table de gauche est celle qui est de cardinalité unique,
- et la table de droite est celle qui est de cardinalité multiple (définissant une relation fonctionnelle gauche → droite)
- L’attribut servant pour la jointure est donc clé étrangère de la table de gauche et clé primaire de la table de droite.
Il y a deux stratégies possibles pour faire une jointure :
- double boucle : c'est l'algorithme le plus simple. La table de droite est examinée une fois pour chaque tuple de la table de gauche. Cette stratégie est facile à implémenter mais peut être très coûteuse. Toutefois, si la table de droite est indexée sur l'attribut qui sert pour la jointure (cas le plus courant), elle peut donner de bons résultats;
- tri-fusion : chaque table est triée sur les attributs de jointure avant que la jointure soit effectuée. Une fois le tri fait, les tables peuvent être fusionnée : chaque table n'est examinée qu'une seule fois (ici, la jointure n'est pas coûteuse, c'est bien sûr sur l'opération de tri que tout est reporté).
Exemple :
On considère les schémas R(a1,a2,a3) et S(a3,a4,a5) ayant l’attribut a3 en commun :
- L’attribut a3 est une clé étrangère du schéma R.
- R est “à gauche” (contient la clé étrangère), et S est “à droite”.
Soient r et s deux tables obéissant aux schémas R et S, et de taille |r| et |s|.
Algo naif :
Pour chaque tuple e de r:
Pour chaque tuple f de s:
Si e(a3)=f(a3):
ajouter e U f à la réponse
Complexité : O (|r| ×|s|)
Si la table de droite est indexée sur l'attribut a3 qui sert pour la jointure, l’algo suivant peut donner de bons résultats :
Pour chaque tuple e de r: # table de gauche x ← e(a3) i ← Index(x) # index sur la table de droite f ← s[i] ajouter e U f à la réponse
- si la recherche dans l'index est en est en log(|s|)
- Complexité : O (|r| × log |s|)
La division
- Soient r (de schémas R) et s (de schémas S), avec S ⊆ R :
La division r ÷ s est la relation (table) u de schéma R-S maximale contenant des tuples tels que u × s ⊆ r (avec × représentant le produit cartésien)
$$r ÷ s = \{ t | ∀ q ∈ s, t \cup q ∈ r\}$$
→ on cherche les éléments de t qui “correspondent” à s
Exemples :
- Liste des pays qui exportent tous les types de matières premières
- Liste des pays qui exportent les mêmes matières premières que l'Arabie Saoudite
- Liste des élèves présents à tous les cours magistraux d'informatique de première année
6.7.4 Recherches composées
- Certaines requêtes, peuvent être le résultat de la combinaison de plusieurs critères de recherche
- La combinaison de résultats est généralement réalisée à l'aide des opérations ensemblistes classiques (intersection, union…) pour exprimer «et», «ou», «non»…
- Pour alléger les formules, il est possible d'utiliser des tables intermédiaires.
- Soient r1 et r2 deux tables de schéma R.
L'union r1 U r2 est une nouvelle table de schéma R constituée de l'ensemble des enregistrements qui appartiennent à r1 ou à r2: $$r1 \cup r2 = { t ∈ r1} \cup { t ∈ r2}$$
- Soient r1 et r2 deux tables de schéma R.
L'intersection r1 ⋂ r2 est une nouvelle table de schéma R constituée de l'ensemble des enregistrements qui appartiennent à r1 et à r2: $$r1 \cap r2 = \{ t ∈ r1\} \cap \{ t ∈ r2\}$$
- Soient r1 et r2 deux tables de schéma R.
La différence r1 - r2 est une nouvelle table de schéma R constituée de l'ensemble des enregistrements qui appartiennent à r1 mais pas à r2: $$r1 - r2 = \{ t ∈ r1\} - \{ t ∈ r2\}$$
Exemples :
- Donner la liste des pays qui exportent à la fois du gaz et du pétrole :
$$\pi _{Pays} σ_\text{matière = gaz} (\text{Exportations}) \cap \pi _{Pays} σ_\text{matière = pétrole} (\text{Exportations})$$ en SQL :
SELECT pays FROM Exportations WHERE matière = 'gaz' INTERSECT ( SELECT pays FROM EXPORTATIONS WHERE matière = 'pétrole');
- Donner la liste des pays qui exportent du gaz mais pas du pétrole :
$$\pi _{Pays} σ_\text{matière = gaz} (\text{Exportations}) - \pi _{Pays} σ_\text{matière = pétrole} (\text{Exportations})$$ en SQL :
SELECT pays FROM Exportations WHERE matière = 'gaz' EXCEPT ( SELECT pays FROM EXPORTATIONS WHERE matière = 'pétrole');
* Donner la liste des clients qui commandent uniquement des produits 'Moxcom' : $$\pi_{nom\_client}Client - \pi_{nom\_client} \sigma_{fournisseur \neq 'Moxcom'} Client ⋈ Commande$$ en SQL :
SELECT nom_client FROM Client EXCEPT ( SELECT client FROM Client NATURAL JOIN Commande WHERE fournisseur <> 'Moxcom');
7. Analyse des données
L’analyse des données a pour but de recomposer l’information contenue dans les données recueillies afin d’en fournir une vue plus synthétique, ou d’extraire des informations qui n’apparaissent pas de façon explicite dans la série de mesures initiale :
Exemples de grandes masses de données :
- Masses de données (pullulantes) : tickets de caisse, clics web, appels tel, operations bancaires, remboursements no URSSAF, trajets SNCF…
- Données importantes : fichiers de clients, données biométriques, campagnes de mesures, sondages,…
- Données géographiquement localisées (gestion d’un “territoire”) : appels tel, centres de production, consommation eau-électricité-gaz, infractions pénales, arrêts maladie, prêts bancaires, allocations chômage, jugements des TGI, accidents du travail…
Le but est de dégager :
- des tendances (covariables)
- des modes de la distribution (présence de plusieurs maxima)
à partir d’un grand ensemble de données (chiffre d’affaires, nb de ventes, masse salariale, …) évoluant dans le temps et dans l’espace, afin de
- définir des indicateurs pertinents
- faciliter la prise de décision.
7.1 L'agrégation
Agrégation
L'agrégation consiste:
- à organiser les données en classes selon la valeur d'un attribut.
- à utiliser des opérateur d’aggrégation :
- comptage, somme, moyenne, ecart-type, max, min, …
- (
count,sum,mean,avg,max,min…)
- afin de dégager :
- des tendances (selon une dimension)
- des modes (analyse par histogramme)
cas d’utilisation :
- Quels sont les catégories de films/livres les plus fréquemment empruntés?
- A quelles heures de la journée la messagerie est-elle la plus sollicitée?
- Comment se répartissent géographiquement les utilisateurs de la messagerie?
SQL
En SQL, l'opérateur d'agrégation est GROUP BY:
- définit des regroupements de données à partir des valeurs de l'attribut mentionné
- il est possible de faire des regroupements selon les valeurs de plusieurs attributs
Exemples de requêtes faisant appel aux fonctions d’agrégation :
Nombre d’élèves par groupe de TD / par prépa d’origine etc..:
SELECT groupe_TD , COUNT(num_eleve) FROM Eleve GROUP BY groupe_TD
Donner les chiffres des ventes du magasin pour chaque mois de l’année
SELECT mois, SUM(montant) FROM Vente GROUP BY mois
Donner le nombre de ventes d’un montant > à 1000 euros pour les mois dont le chiffre d'affaires est supérieur à 10000 euros
SELECT mois, COUNT(num_vente) FROM Vente GROUP BY mois HAVING SUM(montant) >= 10000
Tester les disparités salariales entre hommes et femmes
SELECT sexe, avg( salaire ) FROM Employé GROUP BY sexe
Tester les disparités salariales selon le niveau d’éducation
SELECT niveau_educatif, avg( salaire ) FROM Employé GROUP BY niveau_éducatif
7.2 Découverte d'informations
La découverte d'informations consiste à développer des outils de mise en forme des données facilitant leur analyse. Elle repose sur deux aspects :
- projection de données qualitatives sur des espaces vectoriels ("quantification" des données)
- production d'histogrammes multivariés dans le but d'analyser la distribution des données dans l'espace de reconstruction
Le but est ici de dégager :
- des corrélations (analyse croisée)
Exemples de corrélations :
- Réussite / taux d’embauche / salaire en fonction de la prépa d’origine / sexe / profession des parents
- Tester les disparités salariales hommes/femmes en fonction du niveau d’éducation.
- Donner le taux de réussite aux examens par groupe de matière en fonction de la filière d’origine (MP, PSI, PC, PT, …)
- Y a-t-il une corrélation entre le lancement d’une campagne publicitaire et les chiffres de vente? quels sont les supports les plus efficaces?
Sites de données :
7.2.1 Tables pivot
- Notion de fait élémentaire (fact): transaction ou opération localisée dans le temps et dans l’espace
Remarque : Les transactions marchandes sont un cas classique (acte d’achat bien répertorié et enregistrés, livres de comptes, …)
Exemples de “fait”:
- Achat/Vente
- Opération bancaire (débit/crédit)
- Consultation (site web)
- Souscription à un contrat d’assurance
- Appel téléphonique
- Inscription
Tous ces faits peuvent être localisés. Des mesures peuvent être effectuées sur ces faits (montant d’une vente, durée d’un appel, montant d’une opération bancaire, …)
Points clés :
- distinction entre Dimension et Mesure.
- Notion de dimension : qui? quoi? où? quand? Comment? : associe des coordonnées à l’événement (géographiques, temporelles) et par extension une catégorie.
- Notion de mesure(s) associées à l’événement (exemple : montant de la vente)
- distributions, répartitions, etc… cf analogie proba/stats : événement aléatoire, vecteur aléatoire, …
- les événements sont associés par paquets sur des intervalles réguliers ou selon des catégories discretes.
- Fonctions d’aggrégation : réalise la mesure sur les groupe : somme, comptage, moyenne, min, max, etc…
- histogramme : nb d’événements observés par secteur sur un maillage régulier de l’espace des coordonnées. Par extension mesure sur ce maillage par une fonction d’aggrégation.
- les mesures portent sur des données de type quantitatif
- les classes reposent sur des données de type qualitatif.
Les tables pivot permettent d'analyser des faits selon deux dimensions organisées sur les deux axes d'un tableau.
L'utilisation de données structurées dans un programme Python nécessite de faire appel à des librairies spécialisées. Nous regardons ici la librairie pandas qui sert à la mise en forme et à l'analyse des données.
import numpy as np import matplotlib.pyplot as plt import pandas
Considérons des informations stockées dans un fichier au format ‘csv’ (comma separated values) : ventes_new.csv
On utilise:
pandas.read_csv. Voir dataframes pandas. Pandas permet également de lire les données au formatxlsetxlsx(Excel).
with open('ventes_new.csv') as f: data = pandas.read_csv(f) print(data)
avec data une structure de données de type DataFrame.
exemple : on représente les ventes selon (1) la dimension géographique et (2) la dimension temporelle
T = pandas.pivot_table(data, values = 'MONTANT', index = ['PAYS'], columns = ['ANNEE'], aggfunc=np.sum) print(T)
Evolution des ventes au cours de l'année pour la France seulement:
selection = data[data.PAYS == "France"] T2 = pandas.pivot_table(selection, values = 'MONTANT', index = ['ANNEE'], columns = ['VILLE'], aggfunc=np.sum) print(T2) T2.plot(kind='bar', subplots = 'True') plt.show()
7.2.2 Modèle en étoile
Ici les données sont organisées autour de plusieurs dimensions. L'agrégation consiste:
- à positionner les données sur des axes (temporels, géographiques,…)
- ou à les organiser de manière hiérarchique en classes (et sous-classes) selon la valeur d'un ou plusieurs attributs.
Exemple de hiérarchie:
- pays > région > département
Dimensions
- (qui?) Quels sont les magasins les plus rentables? doit-on ouvrir / fermer des magasins?
- (Où?) répartition des appels/consultation des sites en fonction de l'heure de la journée
- (qui?) Quelle est la liste des clients à contacter?
- (quand?) De quelle quantité doit-on approvisionner quels magasins en fonction de la période de l’année?
Problèmes :
- définir les bons intervalles temporels?? créneaux horaires?
- définir des secteurs géographiques?
Modèle en étoile
- un fait est une association située au centre du schéma. Les attributs de l’association sont les mesures effectuées
- une dimension est une relation participant au fait. Les dimensions sont donc décrites par des attributs (ex : attributs année, trimestre, mois, jour, heure, minute, seconde,…pour une dimension temporelle)
- pour chaque dimension, on décrit une hiérarchie sur les différents attributs de la dimension en définissant un ordre, du particulier au général.
Exemples :
- sur la dimension temporelle : mois ⊂ trimestre ⊂ année
- sur la dimension promotion : nom ⊂ catégorie ⊂ média ⊂ type de média
etc…
Exemples
Cubes de données
Un cube de données est une structure de données organisée sur le principe des espaces vectoriels. Différents axes sont définis, chaque axe étant associé à une dimension particulière.
- Les dimensions peuvent correspondre à des valeurs discrètes (catégories : type de produit, catégorie de client,…) ou continues (valeurs temporelles ou géographiques, …).
- Chaque fait est décrit comme un point de l’espace vectoriel. Il est positionné dans une cellule du cube. A ce point sont associées une ou plusieur mesures.
- Le cube est un ensemble de cellules (voir figure), chaque cellule correspondant à un intervalle (sur les axes continus) ou une valeur (sur les axes discrets).
Un élément essentiel du modèle de données est la définition de hiérarchies sur les dimensions du cube. Chaque dimension se divise en intervalles et sous-intervalles (pour le continu/ quantitatif) ou en catégories et sous-catégories (pour le discret/qualitatif)
Les hiérarchies sur les différentes dimensions permettent de définir le “niveau de résolution” sur les différentes dimensions.
- On peut ainsi s’intéresser à l’évolution d’une certaine grandeur au cours du temps année par année, trimestre par trimestre ou mois par mois selon le niveau de résolution choisi.
- → Hiérarchie : description arborescente d’intervalles et de sous-intervalles sur une dimension. Implemente differentes granularités sur la dimension considérée.
La structure de cube de données est adaptée pour la réalisation d’histogramme multidimensionnels, selon les axes choisis et le niveau de résolution choisi, à l’aide de fonctions d’aggrégation.
- Histogramme et aggrégation
- (vue quantitative) comptage/répartition d’événements sur un intervalle (discrétisaton d’une distribution d’événements)
- (vue qualitative) comptage d’événements par catégorie
- (vue intermediaire) comptage d’événements par catégories hiérarchisées
7.2.2 Mise en oeuvre
XMLA / MDX
7.3 Méthodes avancées
REPRESENTATION DES DONNEES : Représenter des jeux de valeurs de grande taille de façon plus synthétique (algorithmes de réduction de dimension)
REGROUPEMENT (“CLUSTERING”) : Définir des regroupements (ou des classements simples ou hiérarchiques) entre jeux de valeurs
COMPLETION : Méthodes de classification automatique (ou d’interpolation) visant à deviner soit la classe, soit certaines valeurs non mesurées, à partir d’un jeu de valeurs et d’une base d’exemples complets. Il existe des méthodes paramétriques ou non paramétriques.
ESTIMATION ET DECISION : Méthodes visant à estimer la “valeur” associée à un jeu de données (pour l’aide à la décision)