Soit une chaîne de caractères d de longueur n et un mot t de longueur m<n.

1. Donner l'algorithme naïf retournant la position de la première occurrence du mot t dans la chaîne d (ou -1 s'il est absent). Quelle est sa complexité?
2. Donner de même l'algorithme retournant la position de toutes les occurrences du mot t dans la chaîne d (ou une liste vide s'il est absent). Quelle est sa complexité?
3. On suppose qu'on peut tester si un caractère c appartient au motif t en temps constant. Proposez un algorithme plus efficace que l'algorithme naïf.

Algo : recherche_simple 
Données : d, t : chaînes de caractères
    n = len (d)    
    m = len (t)
    i <-- 0
    tant que i < n - m:
        j <-- 0
        tant que j < m et d[i+j] = t[j] :
            j += 1
        si j == m :
           return i
        sinon :
           i <-- i + 1

Algo : recherche_multiple
Données : d, t : chaînes de caractères
    n = len (d)    
    m = len (t)
    l = []
    i <-- 0
    tant que i < n - m:
        j <-- 0
        tant que j < m et d[i+j] = t[j] :
            j += 1
        si j == m :
           l.append(i)
        i <-- i + 1   
    retourner l

RECHERCHE DE CHAINES CODEES EN MACHINE
CHINE
     CHINE
          CHINE
             CHINE
              CHINE
                   CHINE
                        CHINE
                             CHINE
                                 CHINE
RECHERCHE DE CHAINES CODEES EN MACHINE

Algo : recherche améliorée
Données : d, t : chaînes de caractères
    n = len (d)    
    m = len (t)
    i <-- m - 1
    tant que i < n :
      # PRE-TRAITEMENT      
        c = d[i]  
        si c appartient à t:
           k <-- dernière_occurrence(c, t)
           si k == m-1:
               decalage <-- m
           sinon  
               decalage <--  m - 1  - k 
        sinon:
           decalage <-- m
      # TRAITEMENT
      j <-- 0
      tant que j < m :
         si t[m - j - 1] = d[i - j]
            j += 1
         sinon
            break
      si j = m:
        retourner i - m + 1          
      # DECALAGE      
      i <-- i + decalage      
    retourner -1 

1. Écrire un algorithme qui compte le nombre de mots dans un texte.

Remarque : On considère comme caractère d'espacement tout caractère qui n'est pas alphanumérique (alphabétique accentué ou non et chiffres).

2. Dessiner l'automate fini correspondant.

def compte_mots(d):
    state = 0
    cpt = 0
    for i in range(len(d)):
        if state == 0 and is_alpha(d[i]):
            state = 1
            cpt += 1
        if state == 1 and is_sep(d[i]):
            state = 0
    return cpt

1. Écrire un algorithme récursif permettant de savoir si un tableau de caractères est un palindrome (un palindrome se lit "à l'endroit" et "à l'envers" de la même façon, comme par exemple "à l'étape, épate-la!").

Remarque : on ne considère ni la ponctuation, ni les espaces, ni les accents.

Quelle est sa complexité?

2. Pouvez-vous définir un automate fini capable de reconnaître les palindromes?

• Les langages réguliers sont des types de langages formels qui peuvent être reconnus par un automate fini.
• Le langage des expressions régulières est un langage régulier qui permet de décrire des motifs (c'est à dire des classes de mots) dans une chaîne de caractère.

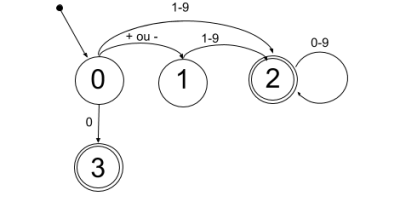
1. Donnez l'expression régulière permettant de reconnaître les entiers relatifs et dessiner l'automate fini correspondant.

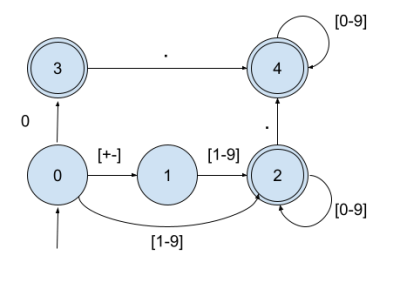
2. Donnez l'expression régulière permettant de reconnaître les nombres décimaux (par exemple -3, 12.3, -12.34, +3, 0.) et dessiner l'automate fini correspondant.

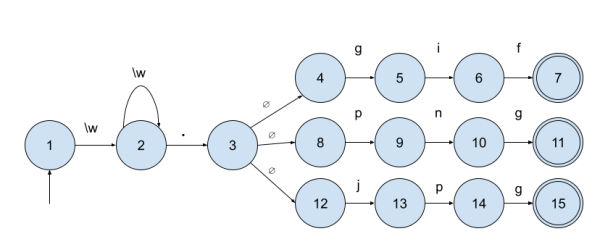
3. Donnez l'expression régulière expression régulière qui valide les noms de fichiers se terminant par l'une des extensions spécifiées : .jpg, .png, ou .gif et dessiner l'automate fini correspondant.

4. Donnez une expression régulière pour reconnaître les URL commençant par https://.

Correction :

https://[a-zA-Z0-9.-]+\.[a-zA-Z]{2,}

5. Écrivez une expression régulière pour reconnaître la date et l'heure au format YYYY-MM-DD (HH:MM) Correction :

\d\d\d\d-(0[1-9]|1[12])-(0[1-9]|[12][0-9]|3[0-1]) \((0[0-9]|1[0-9]|2[0-3]):[0-5][0-9]\)

1. Ecrire l'algorithme de reconnaissance de l'expression régulière (a|b)*c

def reconnait(s):
    final = False
    for c in s:
        if final:
            final = False
            break
        if (c not in 'abc'):
            break
        if c=='c':
            final = True
    return final

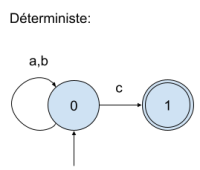
2. Dessiner son automate fini

3. Soit G le graphe orienté décrivant cet automate, chaque arête étant indexée par un caractère. Donner l'algorithme qui indique si oui ou non l'expression est reconnue dans une chaîne s à partir de son automate fini.

G = { 0 : {'a':0, 'b':0, 'c':1}, 1:{}}
 
def reconnait_auto(s, G):
    state = 0
    for c in s:
        if c in G[state]:
            state = G[state][c]
        else:
            return False
    if state == 1:
        return True
    else:
        return False
 

4. Quelle est sa complexité?

Longueur de la chaîne

1. Même exercice avec l'expression régulière (a|b)*ab

def reconnait_nd(s):
    transit_a = False
    final_b = False
    for c in s:
        if (c not in 'ab'):
            break
        if c=='b':
            if transit_a: 
                transit_a = False
                final_b = True
            else:
                final_b = False
        if c == 'a':
            final_b = False
            transit_a = True
    return final_b

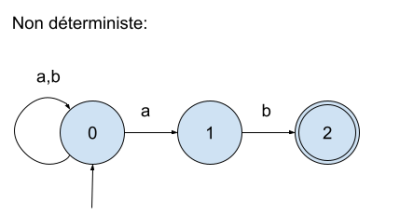
2. Dessiner son automate fini

Voir le graphe G ci-dessous Attention, graphe non déterministe!!

G = { 0 : {'a':(0,1), 'b':(0,)}, 1:{'b':(2,)}, 2:{}}

3. Soit G le graphe orienté décrivant cet automate, chaque arête étant indexée par un caractère. Donner l'algorithme qui indique si oui ou non l'expression est reconnue dans une chaîne s à partir de son automate fini.

def reconnait_auto_nd(s, G):
    states = set((0,))
    for c in s:
        previous_states = states
        states = set()
        for state in previous_states:
            if c in G[state]:          
                next_states = G[state][c]
                for state in next_states:
                    states.add(state)
        print(c, states)
        if len(states) == 0 :
            return False
    if 2 in states:
        return True
    else:
        return False

4. Complexité