Table des matières
Données et modélisation
1. Données persistantes
- Il s'agit par définition des informations qui doivent être conservées entre deux exécutions.
- Avec l’augmentation des capacités de stockage et leur mise en réseau, les quantités de données conservées ont considérablement augmenté au cours des dernières décennies.
- définissant la manière dont les données sont physiquement stockées sur le support,
- autrement dit la méthode de rangement de la série de mesures :
- fichiers,
- répertoires,
- index,
- etc…
- Contrairement à la mémoire primaire (comme la RAM) rapide et volatile (utilisée pour exécuter les programmes en cours), la mémoire secondaire conserve les informations même en l'absence d'alimentation électrique.
- Elle est généralement plus lente que la mémoire primaire, mais offre une capacité de stockage beaucoup plus importante.
- Les exemples courants de mémoire secondaire incluent les disques durs (HDD), les disques SSD, les clés USB, et les supports optiques comme les CD ou DVD.
Fichiers et répertoires
La mémoire secondaire n’est pas directement accessible (les programmes n’ont pas la possibilité d’aller écrire directement sur le disque). Le système d’exploitation assure ainsi l’indépendance du programme par rapport à l’emplacement des données, au travers d’instructions d’entrée/sortie spécialisées.
Pour que les programmes puissent écrire sur le disque, on introduit des objets intermédiaires : les fichiers. Un fichier est caractérisé par (nom, emplacement (volume, arborescence), droit d’accès, taille,…). Il s’agit d’une entité logique. Tout programme utilisant un fichier passe par le système d’exploitation qui, à partir des informations, détermine la localisation des données sur le support.
- Un fichier est une référence vers un ou plusieurs blocs de données, enregistrés sur un support physique.
- Un fichier est caractérisé par son descripteur, constitué de son nom, son chemin d’accès, ses droits d’accès (lecture/écriture/exécution) selon les utilisateurs, sa position sur le support, sa taille, etc…
- La gestion des fichiers est une des fonctions essentielles des systèmes d’exploitation :
- possibilité de traiter et conserver des quantités importantes de données
- possibilité de partager des données entre plusieurs programmes.
- Ouverture : initialisation d'un flux en lecture ou en écriture
- Lecture : consultation des lignes l'une après l'autre (à partir de la première ligne), dans l'ordre où elles ont été écrites sur le support
- Ecriture : ajout de nouvelles données à la suite ou en remplacement des données existantes
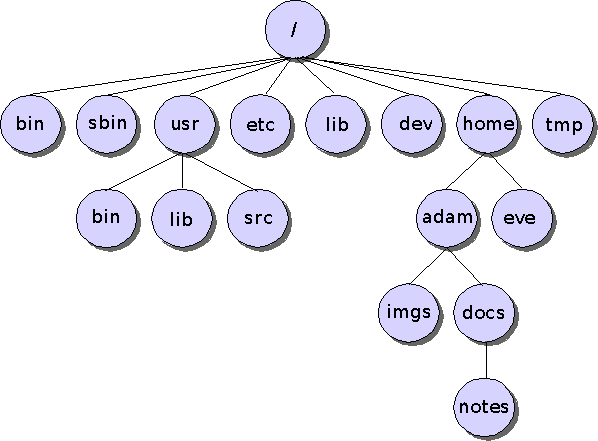
Organisation hiérarchique :
- Lorsque le nombre de fichiers est élevé, les descripteurs de fichiers sont classés dans plusieurs répertoires, organisés sous une forme arborescente.
- Le répertoire de plus bas niveau hiérarchique est appelé racine → chemin d’accès (path)
Consultation des données : lecture d’un fichier (Read)
La consultation des données nécessite d’ouvrir une “communication” entre le programme et les fichiers. Ce canal de communication permet de recevoir un flux de données.
Pour établir la communication, il faut connaître : le “chemin d’accès” aux données (disque dur local) l’”adresse” des données (lorsqu’il s’agit de données stockées sur un serveur distant)
L’opération d’ouverture de fichier initialise un descripteur de fichier, qui sert à désigner (dans le programme) le fichier sur lequel on travaille, et d’accéder au contenu du flux.
FileReader f = new FileReader("/chemin/vers/mon/fichier.txt");
Les opérateurs de lecture et d'écriture ne travaillent pas directement sur les données du fichier. Les données du fichier sont dans une mémoire “tampon”. Lors des opération de lecture, la mémoire tampon est mise à jour au fur et à mesure qu’on avance dans la lecture du fichier par des opérations de lecture sur le disque.
BufferedReader br = new BufferedReader(f);
On utilise la gestion des exceptions permettant de prévoir une action de secours lorsqu’une une opération “risquée” échoue.
Lecture séquentielle
Lorsque l’opération d’ouverture est réalisée avec succès, le flux de données devient accessible en lecture (les premières lignes du fichier sont chargées en mémoire et une tête de lecture se positionne sur le premier caractère de la première ligne). Il ne reste plus qu’à lire les données.
La consultation des données s’effectue séquentiellement à l’aide de l’opérateur de lecture readLine. Chaque appel à cet opérateur charge les nouvelles données et déplace la tête de lecture vers les données suivantes. Cette opération peut être effectuée plusieurs fois jusqu’à atteindre la fin de fichier.
try (BufferedReader br = new BufferedReader(new FileReader("/chemin/vers/mon/fichier.txt"))) { String ligne; while ((ligne = br.readLine()) != null) { System.out.println(ligne); } } catch (IOException e) { e.printStackTrace(); }
Voir aussi :
2. Données structurées
- organisée selon un format ou un schéma prédéfini
- ce qui facilite son stockage, sa manipulation et son analyse.
Tout commence par une fiche à remplir…
Un formulaire se présente sous la forme d’un ensemble de rubriques à remplir.
- Le modèle de fiche définit le format des données à enregistrer:
- liste des rubriques du formulaire,
- domaine de valeurs attendues dans chaque rubrique.
- A toute fiche remplie correspond un jeu de valeurs (ou mesure) :
- liste de valeurs correspondant au contenu d’une fiche particulière.
On peut donc générer à partir d'un modèle de formulaire un grand nombre de données obéissant au même format*
Exemple: un schéma de données décrivant des informations sur des clients avec des colonnes pour le nom, l'adresse, et le numéro de téléphone
Ces données sont généralement stockées dans des formats tabulaires (comme les tableaux ou fichiers CSV) où chaque donnée est placée dans des champs ou colonnes clairement définis.
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
Ce type de données est facilement lisible par les machines et exploitable grâce à des langages de requête.
Formats d'échange
Les principaux formats d'échange de données sont :
- csv
- json
- xml
Chaque enregistrement est codé sur une ligne, chaque valeur étant séparé par un caractère séparateur (virgule, point-virgule, tabulation,…).
Exemple :
Dubois,Martine,"28, rue des Lilas, 45000 Orléans",45
Remarques :
- les données sont des chaînes de caractères
- les guillemets sont nécessaires lorsque la valeur contient le caractère séparateur (ici la virgule)
- les noms des attributs sont éventuellement indiqué sur une ligne séparée
Exemples :
Exemple :
{"nom" : "Dubois", "prénom" : "Martine", "adresse" : "28, rue des Lilas, 45000, Orléans", "âge" : 45}
Remarques :
- reprend la syntaxe du dictionnaire Python
- données numériques ou chaînes de caractères
Pour les données organisées de manière hiérarchique. Des balises servent à séparer les différents attributs.
Ex :
<nom> Dubois </nom> <prénom> Martine </prénom> <adresse> <num> 28 </num> <voie> rue des Lilas </voie> <code postal> 45000 </code postal> <ville> Orléans </ville> </adresse> <âge> 45 </âge>
remarque : le format json permet également de définir des hiérarchies
{
"nom" : "Dubois",
"prénom" : "Martine",
"adresse" :
{
"numero" : 28,
"voie" : "rue des Lilas",
"code_postal" : 45000,
"ville" : "Orléans"
},
"âge" : 45
}
Exemples :
Jeu de valeurs
- une personne réelle : assuré, client, étudiant, auteur, plaignant, contribuable,…
- une personne morale : fournisseur, prestataire, direction, section, promotion,…
- un objet physique : article, véhicule, composant, ingrédient, pièce,…
- un objet contractuel ou administratif : fiche de paye, contrat, procès verbal, billet, dossier…
- un lieu : salle, local, manufacture, entrepôt, ligne de production,…
- un événement : transaction, jugement, achat, vente, acte administratif, appel téléphonique,…
- etc…
- D’un point de vue informatique, un jeu de valeurs recueilli est appelé un enregistrement
- correspondant à l’encodage des données recueillies sur un support numérique
Tuple
Le Tuple est la structure de données de base servant pour le recueil, le transport et le stockage des données.
- Un Tuple est une liste, finie, ordonnée et de taille fixe contenant une suite de valeurs.
- Chaque valeur peut obéir à un format différent
- On note m la taille du tuple (nombre de valeurs)
$$ t = (a_1, ..., a_m) $$ Exemple :
("Dubois", "Martine", 22, "29/10/1994", "Orléans")
3. Indexation
Pour une gestion efficace des données, il est nécessaire de pouvoir identifier chaque jeu de valeurs (tuple) de façon unique.
L'indexation des données repose sur un principe simple d'étiquetage consistant à attribuer une étiquette différente à chaque enregistrement.
- Cette étiquette peut être une suite de caractères arbitraires, un entier, ou un descripteur explicite. On parle en général de clé ou d'identifiant pour désigner cette étiquette.
- Il existe un ordre total dans le domaine de valeurs des clés, permettant d'effectuer des opérations de tri sur les données a partie de la valeur de leur clé.
Définitions et propriétés
- L'indexation des données consiste à attribuer à chaque jeu de valeurs distinct un identifiant unique.
- On parle également de clé de l'enregistrement:
On peut représenter l'opération d'indexation sous la forme d'une fonction. Si $d$ est le jeu de valeurs, $k(d)$ désigne l'identifiant de ce jeu de valeurs.
Unicité/spécificité
L'indexation suppose l'existence d'une bijection entre l'ensemble des données et l'ensemble des clés, permettant d'assurer l'unité et la spécificité de la clé
- soient $d_1$ et $d_2$ deux enregistrements,
- Unicité :
- si $d_1 = d_2$, alors $k(d_1)=k(d_2)$.
- Spécificité:
- si $k(d_1) = k(d_2)$, alors $d_1=d_2$.
Compacité
L'identifiant doit en pratique tenir sur un nombre d'octets le plus petit possible pour que la liste $L$ puisse être manipulée en mémoire centrale. Autrement dit, il faut que :
- $|k| << |d|$
pour que :
- $|L| << |D|$
Efficacité
L'existence d'un identifiant unique pour chaque jeu de valeurs $d$ permet la mise en œuvre d'une recherche par identifiant (ou recherche par clé).
La recherche par identifiant repose sur une fonction d'adressage $I$ (dite "Index") qui à tout identifiant $k$ associe sa position (entrée) $i$ dans un tableau de données: $I : k \rightarrow i$. Ainsi si $k$ est l'identifiant servant à la recherche, l'extraction des informations se fait en 2 étapes:
- $i = I(k)$ (lecture de l'index des données)
- $d = D[i]$ (lecture des données elles mêmes)
- une liste ordonnée de clés (ou toute autre structure ordonnée)
$$L = (k_1, k_2, ..., k_N)$$ telle que $k_1 < k_2 < ... < k_N$, de telle sorte que la recherche dans cette liste s'effectue en O(log N) (recherche dichotomique).
- une table de correspondances qui associe à chaque $k$ l'adresse $i$ correspondante.
Utilisation
Définir un ordre sur les données
La présence d'un identifiant permet de définir un ordre total sur les données :
- ordre sur les entiers (identifiant entier)
- ordre alphabétique (identifiant texte)
- ordre ASCIIbétique (chaîne de caractères quelconque)
Lier les données
Dans le cas des bases de données, l'identifiant constitue une référence vers les jeux de valeurs des tableaux de données. Une référence permet de lier les données d'une table aux données d'une autre table.
Exemple :
- Pour chaque album de la table des albums, l'identifiant d'artiste (ici un numéro) permet de lier l'album avec l'artiste (ou groupe) correspondant.
- Pour chaque piste de la table des pistes, l'identifiant d'album permet de lier la piste à l'album correspondant (et donc à l'artiste correspondant par transitivité)
Structure d'ensemble
L'index définit l'appartenance d'une donnée à un ensemble.
Soit $\mathcal{E}$ un ensemble de données indexées : $$ \mathcal{E} = \{d_1, d_2, ..., d_K\} $$ On a l'équivalence : $$ d \in \mathcal{E} \Leftrightarrow k(d) \in I $$
Ainsi, il ne peut y avoir de doublon car $\forall d$ :
- $k(d)$ est unique
- $i = I(k(d))$ est unique ssi $d \in \mathcal{E}$ et indéfini sinon.
4. Modèle Relationnel
On introduit dans ce chapitre le modèle relationnel qui sert de fondation à la conception de bases de données.
Les différents modèles utiles en représentation des connaissances reposent sur des notions de base de la théorie des ensembles :
- Ensemble finis
- Éléments partiellement (ou totalement) discernables
4.1. Schéma et relation
2 approches en modélisation :
- approche ensembliste (plus général)
- modèle relationnel (plus pratique)
Un tableau de données est une liste (finie et ordonnée) de tuples, chaque tuple obéissant à un même schéma $R$.
Rappel:
- Un enregistrement est un jeu de valeurs organisé sous forme de tuple
- A un tuple on associe en général un schéma de données.
- Définir un schéma consiste à définir :
- une liste d'attributs (labels) associées à chacune des valeurs du tuples.
- A chaque attribut correspond :
- un intitulé
- un domaine de valeurs (type/format des données)
- Soit $R(A_1, ..., A_m)$ un schéma.
- On note $\text{dom}(A_i)$ le domaine associé à l'attribut $A_i$.
- On dit d'un tuple $t$ qu'il obéit au schéma $R$ si les valeurs qu'il contient correspondent aux domaines des attributs du schéma.
Soit $R = (A_1,...,A_m)$ un schéma de données
Une relation $r$ obéissant au schéma $R$ est un sous-ensemble du produit cartésien $\text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- avec :
- $\forall (i,j), a_{ij} \in \text{dom}(A_j), $
- $\forall i, t_i \in \text{dom}(A_1) \times ... \times \text{dom}(A_m)$
- $n$ : nombre de tuples
- $m$ : nombre d'attributs par tuple
- Le schéma $R$ représente le niveau abstrait (modélisation)
- La relation $r$ représente un cas concret de réalisaton (à un schéma $R$ peuvent correspondre une infinité de réalisations possibles : $r$, $r'$, $r''$, etc. )
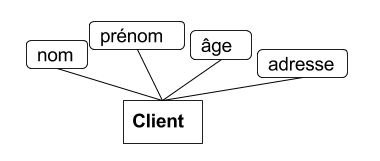
UML :
Client(nom, prénom, adresse, âge)
Étudiant(nom, prénom, adresse, INE)
Ouvrage(titre, auteur, éditeur, prix, date_édition)
Véhicule(immatriculation, marque, modèle, couleur)
4.2. Dépendances fonctionnelles
- Au sein d'un schéma $R$,
- Il peut exister un ensemble de contraintes, noté $F$,
- portant sur les attributs (plus précisément sur les valeurs prises par les attributs).
- L'ensemble F est indépendant de R.
- On parle de contraintes d’intégrité.
- Ces contraintes s’expriment sous la forme de dépendances fonctionnelles.
- Relation binaire : une relation binaire $r$ portant sur deux domaines $\text{dom}(A)$ et $\text{dom}(B)$:
- est un sous-ensemble du produit cartésien $\text{dom}(A) \times \text{dom}(B)$.
- si $(a,b) \in r$, on note parfois $a r b$ ce qui signifie “a est en relation avec b”.
- Fonction : une fonction $f : \text{dom}(A) \rightarrow \text{dom}(B)$ est une relation binaire sur $\text{dom}(A) \times \text{dom}(B)$ telle que
- pour tout $a \in \text{dom}(A)$,
- il existe un unique $b$ tel que $(a,b) \in f$.
- On note $b=f(a)$ ,
- ce qui signifie qu'au sein de la relation $f$, $b$ est déterminé de façon unique par le choix de $a$ (autrement dit : “b dépend de a”)
- Soit $r$ une relation définie selon $R(A_1,...,A_m)$
- Soient $X$ et $Y$ deux sous-ensembles de $R$
- On dit que la relation $r$ définit une dépendance fonctionnelle de $X$ vers $Y$,
- notée $X \stackrel{r}{\rightarrow} Y$
- si les valeurs de $r$ permettent de définir une fonction de $\text{dom}(X)$ vers $\text{dom}(Y)$.
Soit la relation $r$:
| A | B | C |
|---|---|---|
| 1 | a | e |
| 2 | b | f |
| 2 | c | f |
| 3 | d | k |
| 4 | d | k |
- On a les dépendances suivantes :
- $A \rightarrow C$
- $B \rightarrow C$
- mais pas : $A \rightarrow B$, $B \rightarrow A$, ni $C \rightarrow A$
- On a aussi :
- $A,B \rightarrow C$
- mais pas : $B,C \rightarrow A$, ni $A,C \rightarrow B$, etc.
- Soit le schéma :
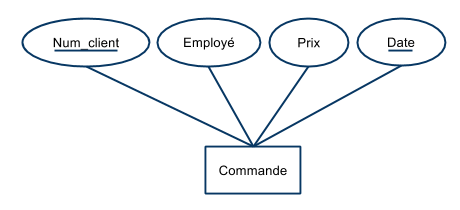
- Commande (num_client, quantité, prix, date, num_article)
- et l’ensemble de contraintes
$$ \begin{array}{rl}F &= \{\\ & \text{num_client, date} \rightarrow \text{num_article, quantité, prix} \\ & \text{num_article, quantité} \rightarrow \text{prix} \\ &\} \end{array} $$
- La première contrainte indique qu'il ne peut y avoir deux factures émises pour un même client à une date donnée.
- La seconde contrainte indique que le prix payé dépend de l’article et de la quantité commandée.
- Soit le schéma :
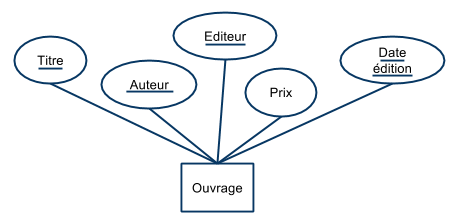
- Ouvrage (titre, auteur, éditeur, prix, date_edition)
- et la contrainte :
- {titre, auteur, éditeur → prix, date_édition}
La contrainte signifie :
- “pour une oeuvre chez un certain éditeur, une seule édition est possible (pas de réédition à une date ultérieure)”
- “politique du prix unique”
- Réservation(code_appareil, date, heure, salle)
Exprimer la dépendance fonctionnelle :
- « Un appareil ne peut pas être utilisé dans deux locaux différents au même moment »
- Il importe donc de bien réfléchir, au moment de l'étape de conception,
- du réalisme et du caractère limitant de certaines dépendances fonctionnelles,
- et du caractère éventuellement limitant du choix des attributs.
- Ainsi, le schéma décrivant les commandes (exemple 2)
- ne permet pas de commander des articles de nature différente au sein d'une même commande
- (un client, pour commander deux râteaux et une truelle, doit donc effectuer deux commandes, qui plus est à des dates différentes!).
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Définir des dépendances fonctionnelles sur cet ensemble d'attributs
4.3 Clé d'une relation
Définitions
- Soit un schéma $R(A_1, ..., A_m)$.
- Une clé $K$ :
- est un ensemble minimal d'attributs inclus dans R,
- tel que toute relation $r$ de schéma $R$ définit une dépendance fonctionnelle de $dom(K)$ dans $dom(R)$,
- cette dépendance est notée $K \rightarrow R$.
- Remarques :
- Si un schéma $R$ possède une clé $K$, alors tous les éléments d’une relation $r$ de schéma $R$ sont discernables : la valeur de la clé permet d’identifier de façon unique chaque élément de l’ensemble.
- Au sein d'un schéma, il est souvent possible de définir plusieurs clés à partir des attributs. Le concepteur du modèle choisit une clé parmi les clés possibles. Cette clé est appelée clé primaire.
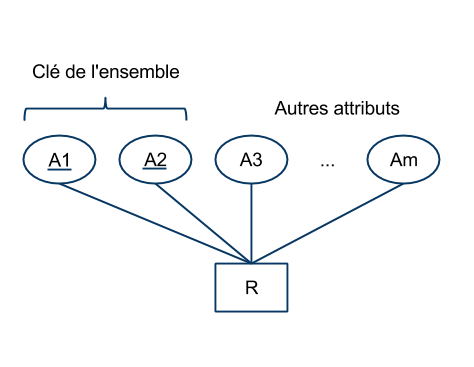
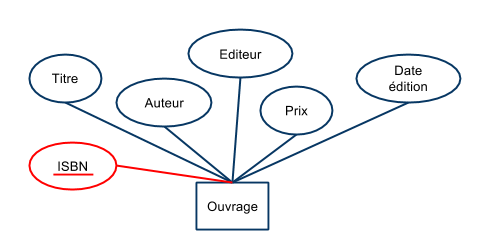
- Graphiquement, les attributs constituant la clé sont soulignés:
- Pour certains schémas,
- il est courant de définir comme clé un entier identifiant de façon unique chaque élément de l'ensemble (appelé identifiant ou “Id”).
- La clé est alors constituée de cet attribut unique.
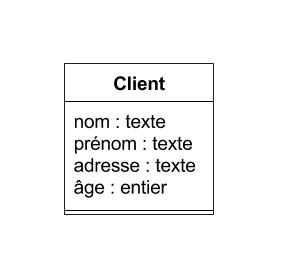
Représentation UML :

Axiomes d'Amstrong
Soit $K$ une clé candidate. On démontre que $K \rightarrow R$ à l'aide des axiomes d'Amstrong à partir d'un ensemble de DF connues:
- Réflexivité : $$Y \subseteq X \Rightarrow X \rightarrow Y$$
- Augmentation : $$X \rightarrow Y \Rightarrow X,Z \rightarrow Y,Z$$
- Transitivité : $$X \rightarrow Y \text{ et } Y \rightarrow Z \Rightarrow X \rightarrow Z$$
- Pseudo-transitivité : $$X \rightarrow Y \text{ et } Y,W \rightarrow Z \Rightarrow X,W \rightarrow Z$$
- Union : $$X \rightarrow Y \text{ et } X \rightarrow Z \Rightarrow X \rightarrow Y,Z$$
- Décomposition : $$X \rightarrow Y, Z \Rightarrow X \rightarrow Y \text{ et } X -> Z$$
Soit le schéma relationnel suivant :
Billet(num_train, type_train, num_voiture, num_place, date, id_passager, nom_passager, prénom_passager, date_naissance, gare_départ , horaire_départ, gare_arrivée, horaire_arrivée, classe, tarif)
Montrer que l'ensemble {num_train, num_voiture, num_place, date, gare_départ} est une clé primaire du schéma?
4.4 Normalisation d'un schéma
Tables mal construites
$$\textbf{Fournisseur}(\underline{\text{nom_f, composant}}, \text{adresse_f, prix})$$
- Problèmes :
- Redondance : l’adresse des fournisseurs est répétée plusieurs fois
- Inconsistance : mauvaise mise à jour ⇒ adresses différentes pour un même fournisseur.
- Problème Insertion : on ne peut pas insérer dans la table un fournisseur qui ne fournit rien
- Problème suppression : si un fournisseur ne fournit plus rien, on perd son adresse
- Solution?
- Couper la table en 2?
–> Impossible de retrouver les prix pratiqués par les différents fournisseurs.
- Nouveau Schéma :
–> Il est possible de reconstruire la table initiale en effectuant une jointure entre ces 2 tables sur l’attribut nom_f.
- Enseignement (id_enseignant, nom_enseignant, matière, id_élève, nom_élève)
- Arrêt (num_train, horaire, nom_gare, ville)
- Facture (id_client, date, article, montant)
Formes Normales
Les Formes normales
- Restreignent les dépendances admises dans un schéma relationnel
- Permettent d’éviter la duplication de l’information au sein des relations
- Définissent une méthode
- de décomposition d’un schéma relationnel redondant
- en plusieurs schémas liés entre eux:
2ème forme normale (2FN)
- Soit $R$ un schéma relationnel
- Soit $X$ un ensemble d’attributs ⊆ $R$
- Soit $A$ un attribut de $R$
- Il existe une DFE entre $X$ et $A$ ssi :
- $X \rightarrow A$
- Il n’existe aucun sous-ensemble $Y$ ⊆ $X$ tel que $Y \rightarrow A$
- Un schéma $R$ est en 2FN :
- ssi la clé primaire de $R$ est en DFE avec tous les autres attributs.
- Donc : il n’y a pas d’attributs qui ne dépendent que d’une partie de la clé.
Normalisation 2FN
- Lorsqu’un schéma relationnel n’est pas en deuxième forme normale, il doit être normalisé:
- Pour obtenir un schéma 2FN:
- on “découpe” la table selon les DFE trouvées entre les attributs de la clé et ceux qui ne sont pas dans la clé.
- La normalisation consiste:
- à créer une nouvelle table pour chaque DFE ainsi trouvée.
- Soit :
$$\mathbf{R} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,\color{red}{B_j},...,B_m)$$
- avec :
$$\color{red}{A_i} \stackrel{DFE}{\rightarrow} \color{red}{B_j}$$ $$A_1,...,\color{red}{A_i},...,A_n \stackrel{DFE}{\rightarrow} B_1,...,B_{j-1},B_{j+1}...,B_m$$
- Alors le schéma de table doit être modifié comme suit :
$$\mathbf{R_1} (\underline{A_1,...,\color{red}{A_i},...,A_n},B_1,...,B_{j-1},B_{j+1}...,B_m)$$ $$\mathbf{R_2} (\underline{\color{red}{A_i}},\color{red}{B_j})$$
Même si aucun attribut ne dépend plus de la clé primaire initiale, il est important de la conserver dans une table spécifique (elle sert à “lier” les valeurs dispersées dans les différentes tables).
- Avant:
$$\textbf{Fournisseur}(\underline{\text{nom_f,composant}}, \text{adresse_f, prix})$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$ $$\text{nom_f, composant} \rightarrow \text{prix}$$
- Après:
$$\textbf{Catalogue}(\underline{\text{nom_f,composant}}, \text{prix})$$ $$\textbf{Fournisseur}(\underline{\text{nom_f}}, \text{adresse_f})$$
- Les tables ont un attribut commun : nom_f (clé primaire de la table Fournisseur).
- La clé primaire de la table des Fournisseurs est dupliquée dans la table des prix (appelée ici Catalogue).
- On dit que nom_f est une clé étrangère de la table des prix (l’attribut fait référence à la clé primaire d’une autre table, en l’occurrence la table des fournisseurs - voir 3.1.1).
3ème forme normale (3FN)
La dépendance fonctionnelle entre 2 attributs $A_i$ et $A_j$ est directe s’il n’existe pas de $A_k$ tel que : $$A_i \rightarrow A_k \rightarrow A_j$$
Un schéma est 3FN :
- S’il est 2FN
- Si tous les attributs sont en DFD avec la clé.
$$\textbf{Commande} (\underline{\text{num_commande}}, \text{nom_f, adresse_f, composant, quantité})$$ $$\text{num_commande} \rightarrow \text{nom_f, composant, quantité}$$ $$\text{nom_f} \rightarrow \text{adresse_f}$$
Le schéma n’est pas 3FN!! (dépendance transitive entre num_commande et adresse)
Normalisation 3FN
* Lorsqu’un schéma relationnel n’est pas en troisième forme normale, il doit être normalisé:
- On crée une table pour chaque DFD trouvée au sein des attributs n'appartenant pas à la clé.
Soit : $$R (\underline{A_1,...,A_m},B_1, ..., \color{red}{B_i},...,\color{red}{B_j},...,B_n)$$ avec : $$A_1, ..., A_m \stackrel{DFD}{\rightarrow} B_1, ...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n$$ $$\color{red}{B_i} \stackrel{DFD}{\rightarrow} \color{red}{B_j}$$ Alors : $$R_1 (\underline{A_1,...,A_m},B_1,...,\color{red}{B_i},...,B_{j-1},B_{j+1},...,B_n)$$ $$R_2 (\underline{\color{red}{B_i}},\color{red}{B_j})$$
Comme précédemment, il est important de conserver la clé primaire de la table initiale si elle permet d'associer les valeurs dispersées dans les tables.
Avant :
- Commande (num_commande, nom_f, adresse_f, composant, quantité)
- avec :
- num_commande → nom_f, composant, quantité
- nom_f → adresse_f
Après :
- Commande (num_commande, nom_f, composant, quantité)
- Client (nom_f, adresse_f)
L’attribut nom_f est maintenant clé primaire de la table Client et clé étrangère de la table Commande.