TP2

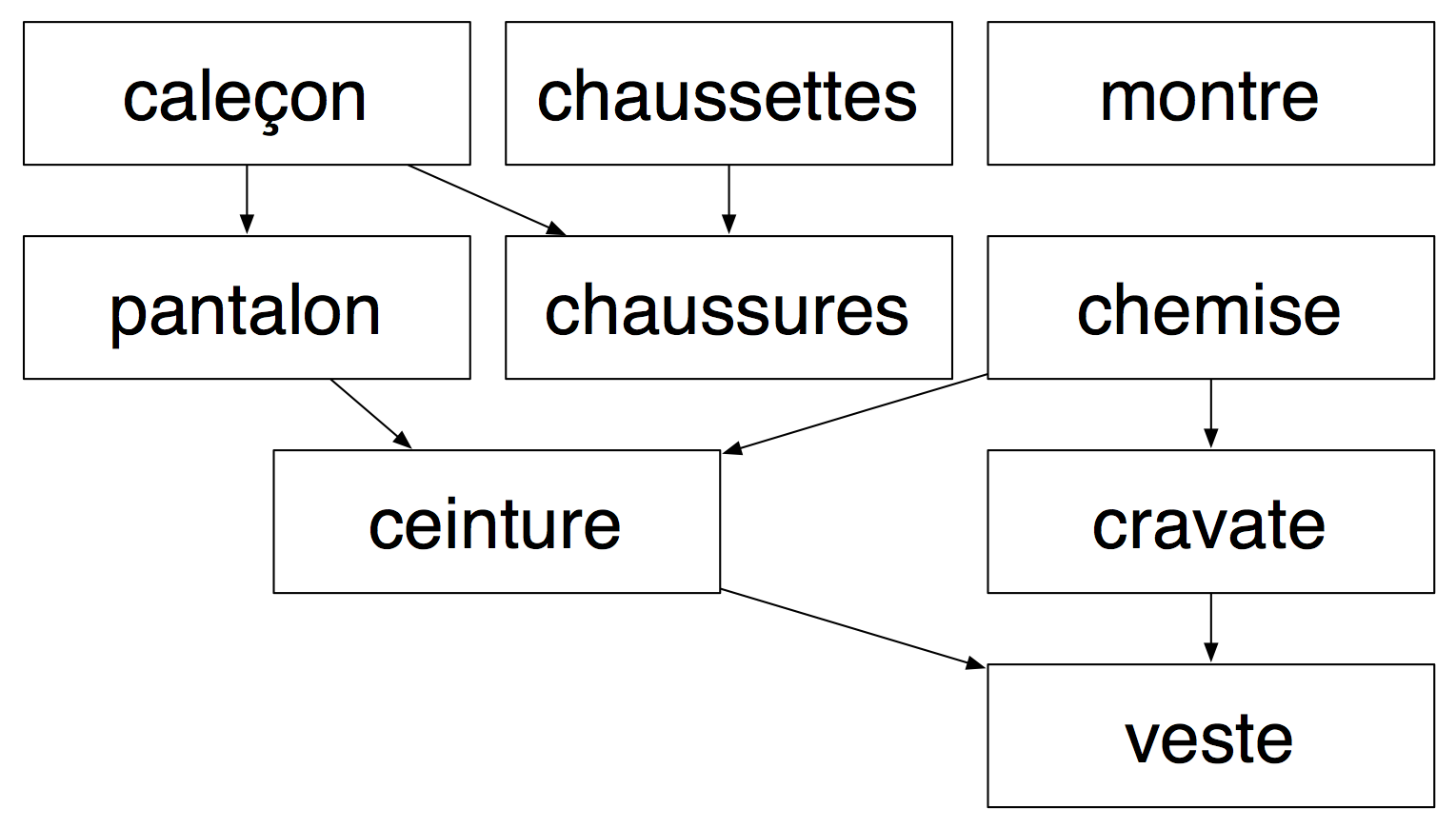
S'habiller le matin. Un ensemble de contraintes possibles :

Le but de ce TP est de résoudre ce problème en proposant un ordre d'habillage possible.

1. Ajoutez au graphe un sommet de départ, voisin de tout les sommets du graphe sur lesquels aucun autre sommet ne pointe
2. Associez un nombre à chaque sommet du graphe (consécutifs et partant de 0)
3. Déduisez-en la Liste d'adjacence du graphe.

Ecrivez la liste d'adjacence du graphe en python (une liste de listes) et testez que c'est le bon graphe (en utilisant ce que vous avez vu dans la partie test du tp 1).

Ainsi, on pourra tester que si g est le graphe :

• g[0] correspond à la liste de tous les voisins de "départ". Il doit y en avoir 4 correspondant aux numéros associés à "caleçon", "chaussettes", "montre" et "chemise" (assert len(g[0]) == 4).
• Si le numéro associé à "pantalon" est 7 et le numéro associé à "ceinture" est 2 alors 2 est dans g[7] (assert 2 in g[7])
• testez deux autres conditions que votre graphe doit avoir.

L'algorithme d'habillage est un dérivé du DFS, que l'on appelle tri topologique.

L'algorithme est récursif et son pseudo code peut être écrit comme suit :

tri_topologique_recursif(s, le_graphe, la_liste_des_sommets_ordonnées, la_liste_des_sommets_marqués):
  placer s dans la liste des sommets marqués
  pour chaque voisin x de s:
    si x n’a pas été marqué:
      tri_topologique(x, le_graphe, la_liste_des_sommets_ordonnées, la_liste_des_sommets_marqués)
  placer s au début de la_liste_des_sommets_ordonnées

Ses paramètres de départ sont :

• s : le sommet de départ,
• le_graphe : le graphe à parcourir,
• la_liste_des_sommets_ordonnées : la liste initialement vide qui contiendra l'ordre topologique après l'exécution de l'algorithme,
• la_liste_des_sommets_marqués : liste initialement vide qui contient les sommet vus pendant l'exécution de l'algorithme.

L'algorithme ne rend rien, il modifie l'objet la_liste_des_sommets_ordonnées au cours de ses différents appels (voir la la partie Modification d'objets dans une fonction pour comprendre comment ça marche).

Pour utiliser l'algorithme, on doit donc créer un objet avec un nom (pour le retrouver) et exécuter l'algorithme. Cet objet sera modifié au court de l'exécution de l'algorithme. Une fois l'algorithme fini, on pourra l'utiliser. Si le sommet de départ est de numéro 0 et que le graphe est codée dans la variable graphe, le code suivant doit fonctionner :

la_liste_des_sommets_ordonnées = []
tri_topologique_recursif(0, graphe, la_liste_des_sommets_ordonnées, [])
print(la_liste_des_sommets_ordonnées)

L'utilisation de paramètres non utiles pour l'utilisateur (la_liste_des_sommets_marqués), ou le fait de se rappeler que le paramètre la_liste_des_sommets_marqués est spécial est source d'erreur pour l'utilisateur. On vous demande d'encapsuler l'algorithme tri_topologique_recursif dans une fonction plus simple nommé tri_topologique.

La fonction tri_topologique doit:

• avoir 2 paramètres : le sommet de départ et le graphe,
• rendre la liste des sommets triés.

Si le sommet de départ est de numéro 0 et que le graphe est codé dans la variable graphe, le code suivant doit fonctionner :

liste_ordonnee = tri_topologique(0, graphe)
print(liste_ordonnee)

Manipuler des nombres peut être pénible pour un être humain. La liste des sommets ordonnés pourrait être mieux décrite par des noms. Pour cela, utilisez une liste dont la valeur à l'indice $i$ correspond au nom du nœud $i$ du graphe et utiliser cette liste pour imprimer les noms triés.

Placer votre graphe et la correspondance nombre, nom dans un fichier à part.

Vous devez avoir cinq fichiers :

• le fichier contenant le graphe,
• le test du graphe,
• le fichier contenant l'algorithme de tri topologique,
• le fichier de test de l'algorithme,
• le fichier contenant l'exécutions de votre programme.

Programmez une machine à calculer (simple : uniquement les 4 opérations de base), d'abord une machine de type HP, puis une machine "normale".