TP4

Le but de ce TP est de résoudre des problèmes d'ordonnancement.

Ici, on suppose que l'on a de l'aide pour s'habiller et que l'on cherche à s'habiller le plus vite possible. On utilisera le même graphe que pour le tp3.

Lors du tp3, vous avez utilisé une structure en liste. Elle nécessitait une correspondance entre des nombres et le vrai nom des sommets (des chaînes de caractères). Nous allons utiliser ici une structure plus simple d'utilisation grâce aux dictionnaires (appelé également tableaux associatifs) et aux ensembles.

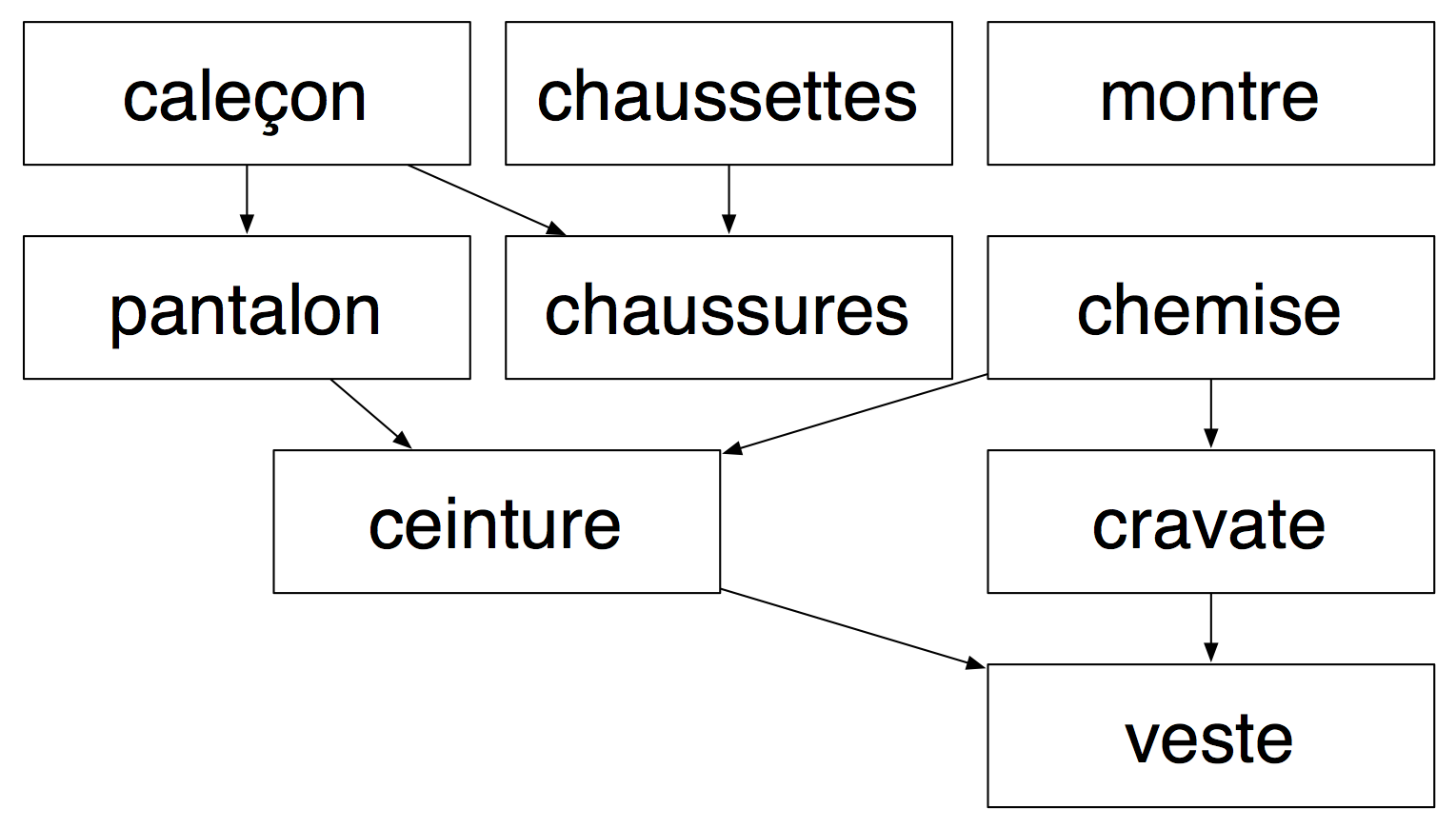
Avec cette structure, on commence par initialiser le graphe et ses sommets :

graphe_habillage = dict()
 
habillage = dict()
 
habillage["caleçon"] = set()
habillage["chaussettes"] = set()
habillage["montre"] = set()
habillage["pantalon"] = set()
habillage["chaussures"] = set()
habillage["chemise"] = set()
habillage["ceinture"] = set()
habillage["cravate"] = set()
habillage["veste"] = set()

La variable habillage (un dictionnaire) contient 9 clés (les sommets du graphes), associés à un ensemble vide (les voisins).

On peut maintenant remplir le graphe avec les voisins. On utilise la méthode add des ensemble qui permet d'ajouter un élément à un ensemble :

habillage["caleçon"].add("pantalon")
habillage["caleçon"].add("chaussures")
 
habillage["chaussettes"].add("chaussures")
 
habillage["pantalon"].add("ceinture")
 
habillage["chemise"].add("ceinture")
habillage["chemise"].add("cravate")
 
habillage["ceinture"].add("veste")
habillage["cravate"].add("veste")

Le graphe est maintenant complet.

On peut alors afficher ses sommets :

for sommet in habillage:
    print(sommet)

Connaître les voisins d'un sommets :

print(habillage["caleçon"])

Connaître tout le graphe:

for sommet in habillage:
    print("le sommet ", sommet, "a pour voisins ", habillage[sommet])

En ordonnancement il n'existe qu'un sommet (appelé départ) qui n'est voisin de personne et qu'un sommet (appelé fin) qui n'a pas de voisins. Ceci n'est pas le cas de notre graphe.

On va automatiser l'ajout d'un sommet départ et fin pour notre graphe :

1. créez deux fonctions :
   • une fonction qui à partir d'un graphe rend l'ensemble des sommets qui ne sont voisins de personne,
   • une fonction qui à partir d'un graphe rend l'ensemble des sommets qui n'ont pas de voisins.
2. mettez à jour le graphe :
   1. ajoutez deux sommets "départ" et "fin" au graphe d'habillage
   2. les voisins de départ sont les sommets rendus par la première fonction,
   3. ajoutez "fin" comme voisin à tous les sommets initialement sans voisins (ceux rendus par la deuxième fonction).

À la fin le code suivant :

for sommet in habillage:
        print("le sommet ", sommet, "a pour voisins ", habillage[sommet])

Doit rendre quelque chose du genre:

le sommet  fin a pour voisins  set()
le sommet  montre a pour voisins  {'fin'}
le sommet  chaussures a pour voisins  {'fin'}
le sommet  cravate a pour voisins  {'veste'}
le sommet  départ a pour voisins  {'montre', 'chemise', 'chaussettes', 'caleçon'}
le sommet  veste a pour voisins  {'fin'}
le sommet  chemise a pour voisins  {'ceinture', 'cravate'}
le sommet  pantalon a pour voisins  {'ceinture'}
le sommet  chaussettes a pour voisins  {'chaussures'}
le sommet  ceinture a pour voisins  {'veste'}
le sommet  caleçon a pour voisins  {'pantalon', 'chaussures'}

Un chemin critique est un chemin le plus long entre les sommets "départ" et "fin".

On utilisera le tri topologique tu tp3, dont une implémentation utilisant les ensemble peut être :

def tri_topologique(sommet_depart, graphe):
 
    def tri_topologique_recursif(s, graphe, sommets_ordonnes_inverse, sommets_marqués):
        sommets_marqués.add(s)
        for voisin in graphe[s]:
            if voisin not in sommets_marqués:
                tri_topologique_recursif(voisin, graphe, sommets_ordonnes_inverse, sommets_marqués)
        sommets_ordonnes_inverse.append(s)
 
    liste_tri_topologique = []
    tri_topologique_recursif(sommet_depart, graphe, liste_tri_topologique, set())
    liste_tri_topologique.reverse()
 
    return liste_tri_topologique

On vous demande d'implémenter la recherche du chemin critique en supposant ici que toutes les tâches sont de durée 1 (vu en td normalement). L'algorithme prend deux paramètres, le graphe (g) et un tri topologique (tri). Son pseudo code peut-être :

# initialisation
pere = dict() 
longueur_chemin = dict() 
pour chaque sommet x du graphe g:
  pere[x] = None # pas de pere pour l'instant
  longueur_chemin[x] = 0 # chemin plus long entre départ et x vaut 0 pour l'instant

# parcours  
pour chaque x de tri:
  pour chaque y de g[x]: 
    si x == "départ":
      durée = 0 # durée de la tâche "départ" 
    sinon:
      durée = 1  # durée de la tâche x
    
    si longueur_chemin[y] ≤ longueur_chemin[x] + durée:
      longueur_chemin[y] = longueur_chemin[x] + durée
      pere[y] = x 

# chemin critique
chemin_critique = []
tache_courante = "fin"
ajoute "fin" au début de chemin critique 

tant que tache_courante != "départ":
  tache_courante = pere[tache_courante]
  ajouter tache_courante au debut de chemin critique 

rendre chemin_critique

Il n'y ici qu'un seul chemin critique :

1. 'départ',
2. 'caleçon',
3. 'pantalon',
4. 'ceinture',
5. 'veste',
6. 'fin'.

Le chemin critique conditionne le temps mis pour exécuter le projet. Chaque tâche de ce chemin doit donc commencer exactement après la tache précédente sinon le projet prendra du retard.

Les autres tâches, en revanche, peuvent commencer une fois que tous ses prédécesseurs ont ́été terminés, mais doivent obligatoirement finir avant le début des tâches qui lui succèdent dans le chemin vers la fin du projet. On renseigne alors pour chaque tâche une date de début au plus tôt et une date de début au plus tard (ces dates sont identiques pour les tâches du chemin critique).

Donné par la valeur de longueur_chemin dans le calcul du chemin critique.

Donnez ces dates pour toutes les tâches.

Elle est déterminée par le chemin le plus long entre ses successeurs et la fin du projet moins le temps pour effectuer cette tâche. On peut calculer cette valeur pour toutes les tâches en parcourant les éléments du tri topologique en partant de la fin. La date de fin d’une tâche est alors le minimum de la date de fin au plus tard de ses successeurs moins la durée de la tâche (ici toujours 1 sauf pour le sommet ”départ” qui est de durée 0). On connaît la date au plus tard du dernier ́élément du tri topologique puisque cet ́élément est le sommet "fin" (il fait parti du chemin critique, donc sa date au plus tôt est ́égal à sa date au plus tard).

Implémentez l'algorithme permettant de calculer les dates au plus tard et donnez-les pour toutes les tâches.